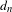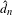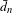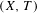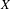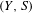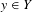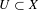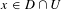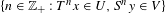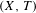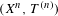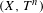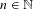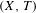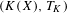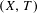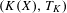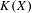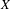24 results
Patterns of polysomnography parameters in 27 neuropsychiatric diseases: An umbrella review – CORRIGENDUM
-
- Journal:
- Psychological Medicine / Volume 54 / Issue 2 / January 2024
- Published online by Cambridge University Press:
- 04 January 2024, p. 435
-
- Article
-
- You have access
- HTML
- Export citation
Polynomial mean complexity and logarithmic Sarnak conjecture
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 769-798
- Print publication:
- March 2024
-
- Article
- Export citation
Patterns of polysomnography parameters in 27 neuropsychiatric diseases: an umbrella review
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 10 / July 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 4675-4695
-
- Article
- Export citation
Periodic points for amenable group actions on uniquely arcwise connected continua
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 30 September 2020, pp. 2833-2844
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Epidemiological features and time-series analysis of influenza incidence in urban and rural areas of Shenyang, China, 2010–2018
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 14 February 2020, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded complexity, mean equicontinuity and discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 494-533
- Print publication:
- February 2021
-
- Article
- Export citation
An answer to Furstenberg’s problem on topological disjointness
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 2467-2481
- Print publication:
- September 2020
-
- Article
- Export citation
A minimal distal map on the torus with sub-exponential measure complexity
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 10 August 2018, pp. 953-974
- Print publication:
- April 2020
-
- Article
- Export citation
When are all closed subsets recurrent?
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 37 / Issue 7 / October 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2223-2254
- Print publication:
- October 2017
-
- Article
- Export citation
Mean equicontinuity and mean sensitivity
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 35 / Issue 8 / December 2015
- Published online by Cambridge University Press:
- 04 August 2014, pp. 2587-2612
- Print publication:
- December 2015
-
- Article
- Export citation
Infinite-step nilsystems, independence and complexity
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 33 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 09 December 2011, pp. 118-143
- Print publication:
- February 2013
-
- Article
- Export citation
Lowering topological entropy over subsets
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 30 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 21 July 2009, pp. 181-209
- Print publication:
- February 2010
-
- Article
- Export citation
Local entropy theory
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 29 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 321-356
- Print publication:
- April 2009
-
- Article
- Export citation
A local variational principle for conditional entropy
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 26 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 13 January 2006, pp. 219-245
- Print publication:
- February 2006
-
- Article
- Export citation
Topological complexity, return times and weak disjointness
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 24 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 04 May 2004, pp. 825-846
- Print publication:
- June 2004
-
- Article
- Export citation
The structure of pointwise recurrent maps having the pseudo orbit tracing property
-
- Journal:
- Nagoya Mathematical Journal / Volume 166 / June 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 83-92
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Homeomorphisms with the whole compacta being scrambled sets
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 21 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 26 March 2001, pp. 77-91
- Print publication:
- February 2001
-
- Article
- Export citation
Non-wandering points and the depth of a graph map
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-152
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Topological entropy of transitive maps of a tree
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 20 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 01 February 2000, pp. 289-314
- Print publication:
- February 2000
-
- Article
- Export citation
Chain recurrent points of a tree map
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 59 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-186
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation