43 results
Review: Comparative methane production in mammalian herbivores
-
- Article
-
- You have access
- HTML
- Export citation
Direct finiteness of certain monoid algebras
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 39 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 20 January 2009, pp. 365-369
-
- Article
-
- You have access
- Export citation
Congruence-free regular semigroups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 28 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 20 January 2009, pp. 113-119
-
- Article
-
- You have access
- Export citation
Decompositions of the congruence lattice of a semigroup
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 23 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-198
-
- Article
-
- You have access
- Export citation
The Idempotent-separating Congruences on a Regular 0-bisimple Semigroup
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 15 / Issue 3 / June 1967
- Published online by Cambridge University Press:
- 20 January 2009, pp. 233-240
-
- Article
-
- You have access
- Export citation
The hypercore of a semigroup
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 28 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-112
-
- Article
-
- You have access
- Export citation
Direct finiteness of certain monoid algebras II
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 39 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 20 January 2009, pp. 371-376
-
- Article
-
- You have access
- Export citation
92.88 Ellipses circumscribing convex quadrilaterals
-
- Journal:
- The Mathematical Gazette / Volume 92 / Issue 525 / November 2008
- Published online by Cambridge University Press:
- 01 August 2016, pp. 566-568
- Print publication:
- November 2008
-
- Article
- Export citation
A property of the complex semigroup algebra of a free monoid
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-104
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
On the contracted l1-algebra of a 0-bisimple inverse semigroup
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 135 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 12 July 2007, pp. 285-295
- Print publication:
- April 2005
-
- Article
- Export citation
Involutions on finite-dimensional algebras over real closed fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 123-128
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
$\mathcal{D}$-FAITHFUL SEMIGROUP-GRADED RINGS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 3 / October 2002
- Published online by Cambridge University Press:
- 14 October 2002, pp. 549-556
-
- Article
-
- You have access
- Export citation
Rings graded by bisimple inverse semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 130 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 11 July 2007, pp. 603-609
- Print publication:
- June 2000
-
- Article
- Export citation
Moore-Penrose inversion in complex contracted inverse semigroup algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-302
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
A note on special involutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 284-288
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
On the l1-algebra of certain monoids
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 128 / Issue 5 / 1998
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1023-1031
- Print publication:
- 1998
-
- Article
- Export citation
Special involutions
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 157-165
-
- Chapter
- Export citation
On the algebra of a free monoid
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 939-945
- Print publication:
- 1996
-
- Article
- Export citation
Trace functions on the algebras of certain E-unitary inverse semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1077-1084
- Print publication:
- 1995
-
- Article
- Export citation
On contracted semigroup rings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 115 / Issue 1-2 / 1990
- Published online by Cambridge University Press:
- 14 November 2011, pp. 109-117
- Print publication:
- 1990
-
- Article
- Export citation



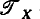 on a set X.
on a set X.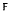 denote a subring of the complex field that contains 1 and is closed under complex conjugation. It is shown that, with respect to the involution induced by word-reversal, the algebra over
denote a subring of the complex field that contains 1 and is closed under complex conjugation. It is shown that, with respect to the involution induced by word-reversal, the algebra over 