36 results
A nonembedding result for complex Grassmann manifolds
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 20 January 2009, pp. 149-153
-
- Article
-
- You have access
- Export citation
New sets of equi-isoclinic n-planes from old
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 20 / Issue 4 / September 1977
- Published online by Cambridge University Press:
- 20 January 2009, pp. 287-291
-
- Article
-
- You have access
- Export citation
Part IV - Information, error and belief
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 393-394
-
- Chapter
- Export citation
List of symbols
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp xxix-xxxii
-
- Chapter
- Export citation
Part III - Here's to probability
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 207-208
-
- Chapter
- Export citation
10 - Random vectors
- from Part III - Here's to probability
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 258-302
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp i-vi
-
- Chapter
- Export citation
2 - How isometries combine
- from Part I - The plane
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 23-42
-
- Chapter
- Export citation
8 - Matrix algebra
- from Part II - Matrix structures
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 162-206
-
- Chapter
- Export citation
Preface
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp xi-xii
-
- Chapter
- Export citation
References
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 832-844
-
- Chapter
- Export citation
5 - The 17 plane patterns
- from Part I - The plane
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 64-78
-
- Chapter
- Export citation
7 - Vectors and matrices
- from Part II - Matrix structures
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 115-161
-
- Chapter
- Export citation
1 - Isometries
- from Part I - The plane
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 3-22
-
- Chapter
- Export citation
4 - Plane patterns and symmetries
- from Part I - The plane
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 48-63
-
- Chapter
- Export citation

Mathematics of Digital Images
- Creation, Compression, Restoration, Recognition
-
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006
Contents
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp vii-x
-
- Chapter
- Export citation
13 - Information and error correction
- from Part IV - Information, error and belief
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 444-520
-
- Chapter
- Export citation
Introduction
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp xiii-xxvi
-
- Chapter
- Export citation
15 - Transforming images
- from Part V - Transforming the image
-
- Book:
- Mathematics of Digital Images
- Published online:
- 05 November 2012
- Print publication:
- 14 September 2006, pp 560-636
-
- Chapter
- Export citation



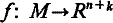 of a differentiable
of a differentiable 