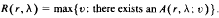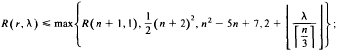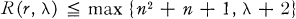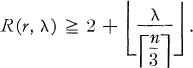13 results
A ‘reg’ palaeosol from the Lower Triassic of south Devon: stratigraphic and palaeoclimatic implications
-
- Journal:
- Geological Magazine / Volume 128 / Issue 5 / September 1991
- Published online by Cambridge University Press:
- 01 May 2009, pp. 517-523
-
- Article
- Export citation
Discussion on a ‘reg’ palaeosol from the Lower Triassic of south Devon: stratigraphic and palaeoclimatic implications
-
- Journal:
- Geological Magazine / Volume 129 / Issue 4 / July 1992
- Published online by Cambridge University Press:
- 01 May 2009, p. 505
-
- Article
- Export citation
Balanced tournament designs with almost orthogonal resolutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-195
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
A note on group divisible designs with mutually orthogonal resolutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-401
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
The existence of a class of Kirkman squares of index 2
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-41
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
A few more balanced Room squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 344-352
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
The number of solutions to an equation arising from a problem on latin squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 1 / February 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-142
- Print publication:
- February 1983
-
- Article
-
- You have access
- Export citation
Equidistant permutation arrays: a bound
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 262-274
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
Resolvable (r, λ)-designs and the Fisher inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 471-478
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
The Asymptotic Behaviour of Equidistant Permutation Arrays
-
- Journal:
- Canadian Journal of Mathematics / Volume 31 / Issue 1 / 01 February 1979
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-48
- Print publication:
- 01 February 1979
-
- Article
-
- You have access
- Export citation
Embedding the affine complement of three intersecting lines in a finite projective plane
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 24 / Issue 4 / December 1977
- Published online by Cambridge University Press:
- 09 April 2009, pp. 458-464
- Print publication:
- December 1977
-
- Article
-
- You have access
- Export citation
Recursive constructions for equidistant permutation arrays
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 24 / Issue 2 / September 1977
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-223
- Print publication:
- September 1977
-
- Article
-
- You have access
- Export citation
A generalization of a theorem of Totten
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 22 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 09 April 2009, pp. 494-500
- Print publication:
- December 1976
-
- Article
-
- You have access
- Export citation



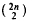 ) distinct unordered pairs of the elements of
) distinct unordered pairs of the elements of