43 results
Combinatorially Factorizable Cryptic Inverse Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 621-630
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
ON WEAKLY AMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 404-417
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
CHARACTERIZING SOME COMPLETELY REGULAR SEMIGROUPS BY THEIR SUBSEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 397-416
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
COMPLETELY REGULAR MONOIDS WITH TWO GENERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 271-287
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Certain characterizations of varieties of bands
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 31 / Issue 2 / June 1988
- Published online by Cambridge University Press:
- 20 January 2009, pp. 301-319
-
- Article
-
- You have access
- Export citation
Congruence lattices of regular semigroups related to kernels and traces
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 34 / Issue 2 / June 1991
- Published online by Cambridge University Press:
- 20 January 2009, pp. 179-203
-
- Article
-
- You have access
- Export citation
A special sublattice of the congruence lattice of a regular semigroup
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 40 / Issue 3 / October 1997
- Published online by Cambridge University Press:
- 20 January 2009, pp. 457-472
-
- Article
-
- You have access
- Export citation
Subdirect products of rings and distributive lattices
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 25 / Issue 2 / June 1982
- Published online by Cambridge University Press:
- 20 January 2009, pp. 155-171
-
- Article
-
- You have access
- Export citation
Canonical Varieties of Completely Regular Semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-104
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Completely 0-simple semigroups of left quotients
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-122
- Print publication:
- December 2004
-
- Article
- Export citation
Orders in completely regular semigroups
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-230
- Print publication:
- December 2001
-
- Article
- Export citation
The kernel relation for an extension of completely 0-simple semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 41 / Issue 2 / May 1999
- Published online by Cambridge University Press:
- 19 July 2001, pp. 211-230
- Print publication:
- May 1999
-
- Article
-
- You have access
- Export citation
Orders in normal bands of groups
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-319
- Print publication:
- December 1996
-
- Article
- Export citation
The kernel relation for a strict extension of certain regular semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 347-357
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
The syntactic monoid of the semigroup generated by a comma-free code
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 1 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 165-179
- Print publication:
- 1995
-
- Article
- Export citation
The kernel and trace operators for ideal extensions of regular semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 219-231
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Congruence networks for completely simple semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-266
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
The congruence lattice of an ideal extension of semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-50
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Operators related to idempotent generated and monoid completely regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-23
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
The modularity of the lattice of varieties of completely regular semigroups and related representations
-
- Journal:
- Glasgow Mathematical Journal / Volume 32 / Issue 2 / May 1990
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-152
- Print publication:
- May 1990
-
- Article
-
- You have access
- Export citation




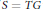
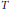
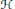
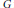
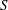
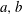
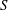
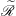
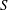
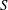
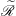
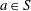

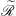
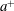


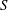
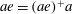
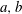
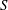
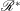
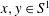
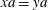
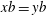
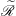
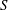
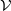
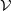
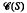 be its congruence lattice. For ρ ∈
be its congruence lattice. For ρ ∈ 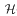 -class of
-class of 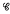 (
(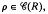 , the kernel of
, the kernel of 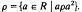 . The relation
. The relation 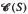 of congruences on a Rees matrix semigroup
of congruences on a Rees matrix semigroup 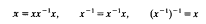
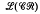 of subvarieties of the variety
of subvarieties of the variety 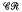 of completely regular semigroups, various results have been obtained which decompose special intervals in
of completely regular semigroups, various results have been obtained which decompose special intervals in 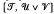 , where
, where 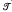 is the trivial variety and
is the trivial variety and 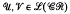 are subdirect products of
are subdirect products of 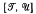 and
and 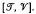 Pastijn and Trotter [13] show that certain intervals of the form
Pastijn and Trotter [13] show that certain intervals of the form 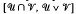 are direct products of the intervals
are direct products of the intervals 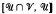 and
and 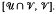 The main objective of this paper is to develop an appropriate lattice theoretic framework for these representations.
The main objective of this paper is to develop an appropriate lattice theoretic framework for these representations.