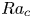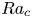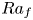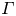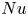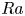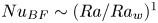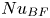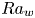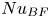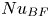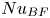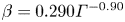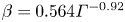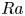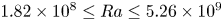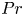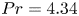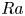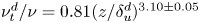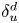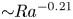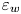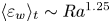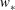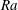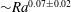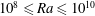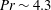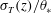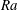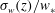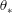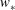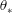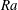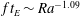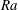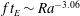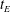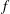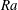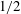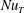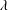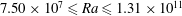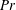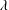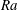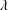44 results
Experimental measurement of spatio-temporally resolved energy dissipation rate in turbulent Rayleigh–Bénard convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 984 / 10 April 2024
- Published online by Cambridge University Press:
- 27 March 2024, A8
-
- Article
- Export citation
Transition to fully developed turbulence in liquid-metal convection facilitated by spatial confinement
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 23 February 2024, R2
-
- Article
- Export citation
Heat transport and flow morphology of geostrophic rotating Rayleigh–Bénard convection in the presence of boundary flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 975 / 25 November 2023
- Published online by Cambridge University Press:
- 22 November 2023, A46
-
- Article
- Export citation
Vortex dynamics in rotating Rayleigh–Bénard convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 974 / 10 November 2023
- Published online by Cambridge University Press:
- 06 November 2023, A43
-
- Article
- Export citation
Heat transfer in a quasi-one-dimensional Rayleigh–Bénard convection cell
-
- Journal:
- Journal of Fluid Mechanics / Volume 973 / 25 October 2023
- Published online by Cambridge University Press:
- 23 October 2023, R5
-
- Article
- Export citation
An experimental study of off-centred rotating thermal convection: a laboratory model for the tidal effects
-
- Journal:
- Journal of Fluid Mechanics / Volume 966 / 10 July 2023
- Published online by Cambridge University Press:
- 29 June 2023, A21
-
- Article
-
- You have access
- HTML
- Export citation
Flow states and heat transport in liquid metal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 25 November 2022
- Published online by Cambridge University Press:
- 28 October 2022, R1
-
- Article
-
- You have access
- HTML
- Export citation
Three-dimensional properties of the viscous boundary layer in turbulent Rayleigh–Bénard convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 947 / 25 September 2022
- Published online by Cambridge University Press:
- 22 August 2022, A15
-
- Article
- Export citation
A laboratory study of internal gravity waves incident upon slopes with varying surface roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 942 / 10 July 2022
- Published online by Cambridge University Press:
- 20 May 2022, A26
-
- Article
-
- You have access
- HTML
- Export citation
Exploring the plume and shear effects in turbulent Rayleigh–Bénard convection with effective horizontal buoyancy under streamwise and spanwise geometrical confinements
-
- Journal:
- Journal of Fluid Mechanics / Volume 940 / 10 June 2022
- Published online by Cambridge University Press:
- 12 April 2022, A37
-
- Article
- Export citation
On the centrifugal effect in turbulent rotating thermal convection: onset and heat transport
-
- Journal:
- Journal of Fluid Mechanics / Volume 938 / 10 May 2022
- Published online by Cambridge University Press:
- 21 March 2022, R1
-
- Article
- Export citation
The effect of tidal force and topography on horizontal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 932 / 10 February 2022
- Published online by Cambridge University Press:
- 09 December 2021, A38
-
- Article
- Export citation
Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 570 / 10 January 2007
- Published online by Cambridge University Press:
- 14 October 2021, pp. 479-489
-
- Article
- Export citation
On the effective horizontal buoyancy in turbulent thermal convection generated by cell tilting
-
- Journal:
- Journal of Fluid Mechanics / Volume 914 / 10 May 2021
- Published online by Cambridge University Press:
- 05 March 2021, A15
-
- Article
-
- You have access
- HTML
- Export citation
Universal fluctuations in the bulk of Rayleigh–Bénard turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 878 / 10 November 2019
- Published online by Cambridge University Press:
- 06 September 2019, R1
-
- Article
- Export citation
Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 877 / 25 October 2019
- Published online by Cambridge University Press:
- 19 August 2019, R1
-
- Article
- Export citation
Tuning heat transport via boundary layer topographies
-
- Journal:
- Journal of Fluid Mechanics / Volume 876 / 10 October 2019
- Published online by Cambridge University Press:
- 31 July 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Moisture transfer by turbulent natural convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 874 / 10 September 2019
- Published online by Cambridge University Press:
- 15 July 2019, pp. 1041-1056
-
- Article
- Export citation
Quasistatic magnetoconvection: heat transport enhancement and boundary layer crossing
-
- Journal:
- Journal of Fluid Mechanics / Volume 870 / 10 July 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 519-542
-
- Article
- Export citation
Turbulent thermal convection over rough plates with varying roughness geometries
-
- Journal:
- Journal of Fluid Mechanics / Volume 825 / 25 August 2017
- Published online by Cambridge University Press:
- 21 July 2017, pp. 573-599
-
- Article
- Export citation