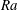We present an experimental study of the reversal of the large-scale circulation (LSC) in quasi-two-dimensional turbulent Rayleigh–Bénard convection. It is found that there exists a transition in the Rayleigh number ($Ra$) dependence of the reversal rate 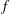$f$ with two distinct scalings: for 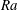$Ra$ less than a transitional value 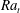$Ra_{t}$, the non-dimensionalized reversal rate 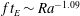$ft_{E}\sim Ra^{-1.09}$; however, for higher 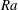$Ra$ the scaling changes to 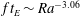$ft_{E}\sim Ra^{-3.06}$, where 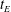$t_{E}$ is the turnover time of the LSC. Flow visualization shows that this regime transition originates from a change in flow topology from a single-roll state to a new, less stable, abnormal single-roll state with substructures inside the single roll. The emergence of the substructures inside the LSC lowers the energy barrier for the flow reversals to occur and leads to a slower decay of 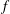$f$ with 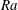$Ra$. Detailed analysis reveals that, although it is the corner rolls that trigger the reversal event, the probability for the occurrence of reversals mainly depends on the stability of the LSC. This is supported by a model we proposed to predict the critical condition for the transition, which agrees well with the experimental results.