1 Introduction
Most fluid flows over large scales in nature are thermally driven, and therefore are convective in nature. Examples include planetary and stellar convections, convections in the atmosphere and the oceans, and mantle and core convections of the Earth. Studying thermal convection thus becomes essential in understanding many of the large-scale fluid phenomena occurring in geophysical and astrophysical systems. A paradigmatic model for thermal convection is the so-called Rayleigh–Bénard (RB) system, a fluid layer heated from below and cooled from above (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010). A central issue in the study of RB convection is how heat is transported by turbulent flows when the flow itself is thermally driven, which is often framed as a scaling relation,
 $Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
, between the Nusselt number
$Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
, between the Nusselt number
 $Nu$
(the non-dimensional heat flux) and the Rayleigh number
$Nu$
(the non-dimensional heat flux) and the Rayleigh number
 $Ra$
(the non-dimensional driving force). Specifically, one asks what is the value of the exponent
$Ra$
(the non-dimensional driving force). Specifically, one asks what is the value of the exponent
 $\unicode[STIX]{x1D6FD}$
for convective flows at the very large values of
$\unicode[STIX]{x1D6FD}$
for convective flows at the very large values of
 $Ra$
that are thought to be relevant to geophysical and astrophysical flows. As current experiments and simulations cannot reach such high values of
$Ra$
that are thought to be relevant to geophysical and astrophysical flows. As current experiments and simulations cannot reach such high values of
 $Ra$
, extrapolations are needed to bridge the gap. However, this can only be done with some confidence if one knows that the asymptotic state, known as the ultimate state of thermal convection, has been reached. Such a state was first suggested by Kraichnan (Reference Kraichnan1962), who argued that when the boundary layers (BLs) become fully turbulent under sufficiently strong thermal driving, heat will be transported ballistically across the fluid layer, resulting in
$Ra$
, extrapolations are needed to bridge the gap. However, this can only be done with some confidence if one knows that the asymptotic state, known as the ultimate state of thermal convection, has been reached. Such a state was first suggested by Kraichnan (Reference Kraichnan1962), who argued that when the boundary layers (BLs) become fully turbulent under sufficiently strong thermal driving, heat will be transported ballistically across the fluid layer, resulting in
 $Nu\sim Ra^{1/2}$
(the existence of a logarithmic correction, however, results in a smaller effective exponent). In contrast, a pure
$Nu\sim Ra^{1/2}$
(the existence of a logarithmic correction, however, results in a smaller effective exponent). In contrast, a pure
 $1/2$
state is now called the asymptotic ultimate state (Grossmann & Lohse Reference Grossmann and Lohse2011). Despite much effort made in the search for the ultimate state, and reports for evidence of it, debates still continue regarding its existence. One way to achieve the ultimate state is to remove the BL in what is called homogeneous convection, which was first demonstrated numerically by Lohse & Toschi (Reference Lohse and Toschi2003), and later experimentally by Gibert et al. (Reference Gibert, Pabiou, Chillà and Castaing2006). In both cases a
$1/2$
state is now called the asymptotic ultimate state (Grossmann & Lohse Reference Grossmann and Lohse2011). Despite much effort made in the search for the ultimate state, and reports for evidence of it, debates still continue regarding its existence. One way to achieve the ultimate state is to remove the BL in what is called homogeneous convection, which was first demonstrated numerically by Lohse & Toschi (Reference Lohse and Toschi2003), and later experimentally by Gibert et al. (Reference Gibert, Pabiou, Chillà and Castaing2006). In both cases a
 $Nu\sim Ra^{1/2}$
was observed. A different approach is to retain the BLs, but add roughness to the surface of the top and bottom plates of the convection cell. The idea is that the roughness may help to trigger a transition to a turbulent BL at a lower
$Nu\sim Ra^{1/2}$
was observed. A different approach is to retain the BLs, but add roughness to the surface of the top and bottom plates of the convection cell. The idea is that the roughness may help to trigger a transition to a turbulent BL at a lower
 $Ra$
. Indeed, the value
$Ra$
. Indeed, the value
 $\unicode[STIX]{x1D6FD}=1/2$
has been obtained in experiments (Roche et al.
Reference Roche, Castaing, Chabaud and Hébral2001; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011; Xie & Xia Reference Xie and Xia2017). But direct numerical simulations (DNSs) of RB convection with rough surfaces in two dimensions found that
$\unicode[STIX]{x1D6FD}=1/2$
has been obtained in experiments (Roche et al.
Reference Roche, Castaing, Chabaud and Hébral2001; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011; Xie & Xia Reference Xie and Xia2017). But direct numerical simulations (DNSs) of RB convection with rough surfaces in two dimensions found that
 $\unicode[STIX]{x1D6FD}$
will fall back from
$\unicode[STIX]{x1D6FD}$
will fall back from
 $1/2$
to
$1/2$
to
 $1/3$
(the so-called classical scaling) when
$1/3$
(the so-called classical scaling) when
 $Ra$
becomes even higher (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). This suggests that the observed
$Ra$
becomes even higher (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). This suggests that the observed
 $1/2$
scaling is not related to the ultimate state that should survive at arbitrarily high
$1/2$
scaling is not related to the ultimate state that should survive at arbitrarily high
 $Ra$
once the system reached that state.
$Ra$
once the system reached that state.
2 Overview
Studying the effect of surface roughness in turbulent thermal convection is not new. The experiment by Shen, Tong & Xia (Reference Shen, Tong and Xia1996) was perhaps the first such study in the context of RB convection. This is followed by experiments made by Ciliberto & Laroche (Reference Ciliberto and Laroche1999), Du & Tong (Reference Du and Tong2000), Roche et al. (Reference Roche, Castaing, Chabaud and Hébral2001) and Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005). In these early studies, a general finding is that heat transport is enhanced once the thermal BL thickness becomes thinner than the roughness height; whether the scaling exponent
 $\unicode[STIX]{x1D6FD}$
changes or not depends on the details of the rough plates (for a brief review on these earlier studies, see, for example, Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014)).
$\unicode[STIX]{x1D6FD}$
changes or not depends on the details of the rough plates (for a brief review on these earlier studies, see, for example, Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014)).
According to the Grossmann–Lohse theory, the kinetic energy and thermal variance dissipation rates can be split into contributions from the bulk and the BLs, and when the dissipation is bulk-dominated
 $Nu\sim Ra^{1/2}$
asymptotically, whereas when BLs become dominant
$Nu\sim Ra^{1/2}$
asymptotically, whereas when BLs become dominant
 $Nu\sim Ra^{1/3}$
, again asymptotically (Grossmann & Lohse Reference Grossmann and Lohse2000). So, by perturbing the BL with surface roughness, one can reduce the BL contribution in the total dissipation and therefore change the overall heat transport to a more bulk-dominated behaviour. Based on this idea, Xie & Xia (Reference Xie and Xia2017) investigated experimentally using a series of convection cells with varying roughness topographies, which would introduce varying levels of BL perturbation. Indeed, they found that the value of
$Nu\sim Ra^{1/3}$
, again asymptotically (Grossmann & Lohse Reference Grossmann and Lohse2000). So, by perturbing the BL with surface roughness, one can reduce the BL contribution in the total dissipation and therefore change the overall heat transport to a more bulk-dominated behaviour. Based on this idea, Xie & Xia (Reference Xie and Xia2017) investigated experimentally using a series of convection cells with varying roughness topographies, which would introduce varying levels of BL perturbation. Indeed, they found that the value of
 $\unicode[STIX]{x1D6FD}$
can be tuned by the roughness topography. They further identified two scaling regimes in the heat-transport-enhanced regime, termed as regime II (corresponding to the thermal BL becoming submerged below the roughness height) and regime III (even the viscous BL becoming submerged; in contrast, regime I corresponds to both BLs being above the roughness height). By defining a roughness parameter
$\unicode[STIX]{x1D6FD}$
can be tuned by the roughness topography. They further identified two scaling regimes in the heat-transport-enhanced regime, termed as regime II (corresponding to the thermal BL becoming submerged below the roughness height) and regime III (even the viscous BL becoming submerged; in contrast, regime I corresponds to both BLs being above the roughness height). By defining a roughness parameter
 $\unicode[STIX]{x1D706}$
, i.e. the aspect ratio of the roughness elements, they showed that when
$\unicode[STIX]{x1D706}$
, i.e. the aspect ratio of the roughness elements, they showed that when
 $\unicode[STIX]{x1D706}$
changed from 0.5 to 4, the corresponding value of
$\unicode[STIX]{x1D706}$
changed from 0.5 to 4, the corresponding value of
 $\unicode[STIX]{x1D6FD}$
in regime II (a transient regime) changed from 0.36 to 0.59, and it changed from 0.3 to 0.5 in regime III (see, for example, figure 1(a) for the case with
$\unicode[STIX]{x1D6FD}$
in regime II (a transient regime) changed from 0.36 to 0.59, and it changed from 0.3 to 0.5 in regime III (see, for example, figure 1(a) for the case with
 $\unicode[STIX]{x1D706}=4.0$
). As
$\unicode[STIX]{x1D706}=4.0$
). As
 $Ra$
of the experiment is well below that at which one would expect to see the ultimate state, the observed
$Ra$
of the experiment is well below that at which one would expect to see the ultimate state, the observed
 $Nu\sim Ra^{1/2}$
scaling is clearly not related to the asymptotic state. Rather, this study demonstrates that one can tune the roughness topography to obtain a desired value of
$Nu\sim Ra^{1/2}$
scaling is clearly not related to the asymptotic state. Rather, this study demonstrates that one can tune the roughness topography to obtain a desired value of
 $\unicode[STIX]{x1D6FD}$
. The
$\unicode[STIX]{x1D6FD}$
. The
 $1/2$
scaling has also be obtained in 2-D DNS studies by Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) and Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017). While in the former the authors believe their results evidence a transition to the ultimate state, in the latter the authors demonstrate, surprisingly, that at even higher
$1/2$
scaling has also be obtained in 2-D DNS studies by Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) and Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017). While in the former the authors believe their results evidence a transition to the ultimate state, in the latter the authors demonstrate, surprisingly, that at even higher
 $Ra$
, the scaling exponent will fall back to the classical
$Ra$
, the scaling exponent will fall back to the classical
 $1/3$
scaling (figure 1
b), which implies that the observed
$1/3$
scaling (figure 1
b), which implies that the observed
 $1/2$
scaling should not be related to the ultimate state.
$1/2$
scaling should not be related to the ultimate state.
By taking a different route than many of the previous studies that use monoscale roughness, Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) adopted a multiscale roughness topography in their simulation. By doing so, they find a
 $1/2$
scaling over three decades of
$1/2$
scaling over three decades of
 $Ra$
from
$Ra$
from
 $1\times 10^{8}$
to
$1\times 10^{8}$
to
 $1\times 10^{11}$
(figure 1
b). They show that the thermal BL is protruded by the three roughness heights sequentially (see the title image): at small
$1\times 10^{11}$
(figure 1
b). They show that the thermal BL is protruded by the three roughness heights sequentially (see the title image): at small
 $Ra$
, all the roughness elements are submerged inside the thermal BL; with increasing
$Ra$
, all the roughness elements are submerged inside the thermal BL; with increasing
 $Ra$
, part of the roughness elements protrude the thermal BL, with the smaller roughness still being submerged in the thermal BL; at the largest
$Ra$
, part of the roughness elements protrude the thermal BL, with the smaller roughness still being submerged in the thermal BL; at the largest
 $Ra$
, the thermal BL follows the surface roughness, acting as a effective smooth surface, resulting in the classical
$Ra$
, the thermal BL follows the surface roughness, acting as a effective smooth surface, resulting in the classical
 $1/3$
scaling (figure 1
b). This represents a new approach to perturb the BL in controlling heat transport scaling. In the simulation by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019), a three-level fractal-like structure was used, but in principle the level of scales is only limited by computational resources. One may then obtain a wider range of a
$1/3$
scaling (figure 1
b). This represents a new approach to perturb the BL in controlling heat transport scaling. In the simulation by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019), a three-level fractal-like structure was used, but in principle the level of scales is only limited by computational resources. One may then obtain a wider range of a
 $1/2$
scaling with a hierarchy of roughness scales. A similar approach can be taken for other scaling exponents (for example, with different values of
$1/2$
scaling with a hierarchy of roughness scales. A similar approach can be taken for other scaling exponents (for example, with different values of
 $\unicode[STIX]{x1D706}$
and multiscale roughness), making it possible to ‘design’ thermal convection systems with specific heat transport scalings.
$\unicode[STIX]{x1D706}$
and multiscale roughness), making it possible to ‘design’ thermal convection systems with specific heat transport scalings.
3 Future
Although both experimental and DNS studies show convincingly that the heat transport in turbulent convection can be tuned by manipulating the boundary layer topographies, there are differences between the 3-D experiments and 2-D simulations. The falling-back of
 $\unicode[STIX]{x1D6FD}$
from
$\unicode[STIX]{x1D6FD}$
from
 $1/2$
to the classical value of
$1/2$
to the classical value of
 $1/3$
for
$1/3$
for
 $Ra>2\times 10^{9}$
observed by Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) is not seen in experiments up to
$Ra>2\times 10^{9}$
observed by Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) is not seen in experiments up to
 $Ra\approx 1\times 10^{11}$
(Xie & Xia Reference Xie and Xia2017). Therefore, experimental studies with
$Ra\approx 1\times 10^{11}$
(Xie & Xia Reference Xie and Xia2017). Therefore, experimental studies with
 $Ra$
larger than
$Ra$
larger than
 $1\times 10^{11}$
will be needed to complete the picture. The physical mechanism leading to the observed relation between
$1\times 10^{11}$
will be needed to complete the picture. The physical mechanism leading to the observed relation between
 $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
 $\unicode[STIX]{x1D706}$
is not fully understood. To this end, studies on the spatial distribution of the energy dissipation rate and the thermal dissipation rate for different roughness configurations should provide some insight, which can only be done with realistic prospects using 3-D DNS. Moreover, the Prandtl number
$\unicode[STIX]{x1D706}$
is not fully understood. To this end, studies on the spatial distribution of the energy dissipation rate and the thermal dissipation rate for different roughness configurations should provide some insight, which can only be done with realistic prospects using 3-D DNS. Moreover, the Prandtl number
 $Pr$
, which characterises the relative thickness of the thermal BL to the viscous BL, is found to have a large impact on the heat transport in rough surface cells (Xie & Xia Reference Xie and Xia2017). Studies with a wider range of
$Pr$
, which characterises the relative thickness of the thermal BL to the viscous BL, is found to have a large impact on the heat transport in rough surface cells (Xie & Xia Reference Xie and Xia2017). Studies with a wider range of
 $Pr$
will thus complement our understanding of turbulent convection over rough surfaces. Finally, a crucial step towards real applications is the experimental realisation of the observations by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) in turbulent convection with multiscale roughness. With their tuning method, it is possible to design systems with desired heat transport efficiencies, which should find many practical applications.
$Pr$
will thus complement our understanding of turbulent convection over rough surfaces. Finally, a crucial step towards real applications is the experimental realisation of the observations by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) in turbulent convection with multiscale roughness. With their tuning method, it is possible to design systems with desired heat transport efficiencies, which should find many practical applications.
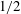 $1/2$ can be achieved for an extended range of the Rayleigh number, providing a new way to manipulate heat transport by tuning boundary topographies in turbulent flows.
$1/2$ can be achieved for an extended range of the Rayleigh number, providing a new way to manipulate heat transport by tuning boundary topographies in turbulent flows.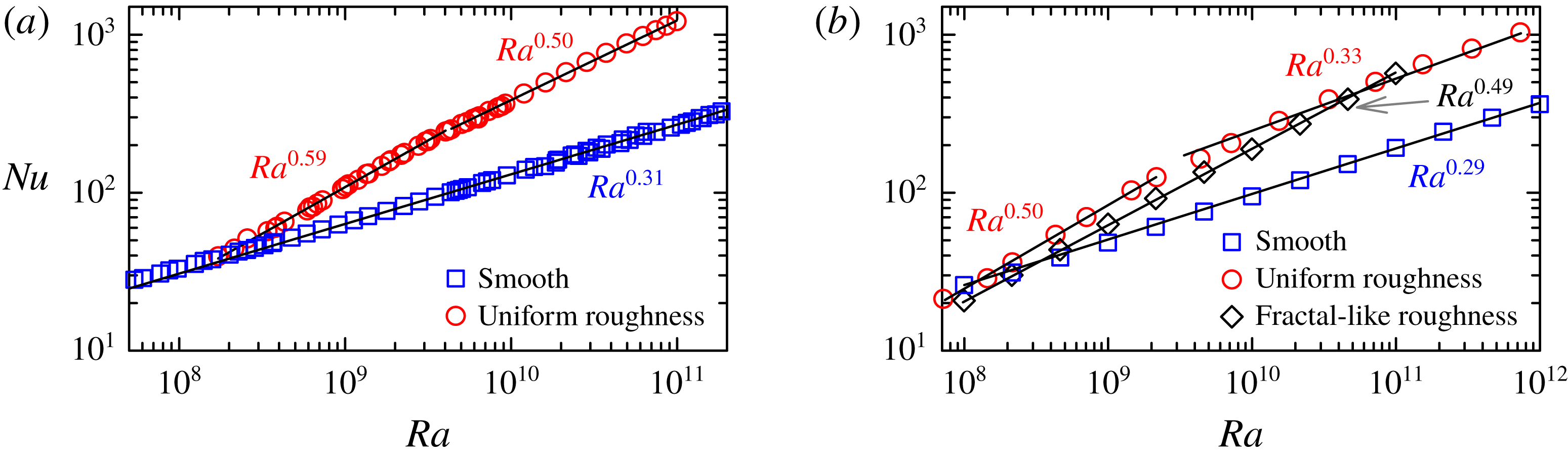
$Nu$ versus
$Ra$ with smooth and rough boundaries. (a) Three-dimensional (3-D) experiments (Xie & Xia 2017) and (b) two-dimensional (2-D) DNS (Zhu et al.2019). The solid lines are power-law fits to the respective data sets.





1 Introduction
Most fluid flows over large scales in nature are thermally driven, and therefore are convective in nature. Examples include planetary and stellar convections, convections in the atmosphere and the oceans, and mantle and core convections of the Earth. Studying thermal convection thus becomes essential in understanding many of the large-scale fluid phenomena occurring in geophysical and astrophysical systems. A paradigmatic model for thermal convection is the so-called Rayleigh–Bénard (RB) system, a fluid layer heated from below and cooled from above (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010). A central issue in the study of RB convection is how heat is transported by turbulent flows when the flow itself is thermally driven, which is often framed as a scaling relation, $Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
, between the Nusselt number
$Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
, between the Nusselt number
 $Nu$
(the non-dimensional heat flux) and the Rayleigh number
$Nu$
(the non-dimensional heat flux) and the Rayleigh number
 $Ra$
(the non-dimensional driving force). Specifically, one asks what is the value of the exponent
$Ra$
(the non-dimensional driving force). Specifically, one asks what is the value of the exponent
 $\unicode[STIX]{x1D6FD}$
for convective flows at the very large values of
$\unicode[STIX]{x1D6FD}$
for convective flows at the very large values of
 $Ra$
that are thought to be relevant to geophysical and astrophysical flows. As current experiments and simulations cannot reach such high values of
$Ra$
that are thought to be relevant to geophysical and astrophysical flows. As current experiments and simulations cannot reach such high values of
 $Ra$
, extrapolations are needed to bridge the gap. However, this can only be done with some confidence if one knows that the asymptotic state, known as the ultimate state of thermal convection, has been reached. Such a state was first suggested by Kraichnan (Reference Kraichnan1962), who argued that when the boundary layers (BLs) become fully turbulent under sufficiently strong thermal driving, heat will be transported ballistically across the fluid layer, resulting in
$Ra$
, extrapolations are needed to bridge the gap. However, this can only be done with some confidence if one knows that the asymptotic state, known as the ultimate state of thermal convection, has been reached. Such a state was first suggested by Kraichnan (Reference Kraichnan1962), who argued that when the boundary layers (BLs) become fully turbulent under sufficiently strong thermal driving, heat will be transported ballistically across the fluid layer, resulting in
 $Nu\sim Ra^{1/2}$
(the existence of a logarithmic correction, however, results in a smaller effective exponent). In contrast, a pure
$Nu\sim Ra^{1/2}$
(the existence of a logarithmic correction, however, results in a smaller effective exponent). In contrast, a pure
 $1/2$
state is now called the asymptotic ultimate state (Grossmann & Lohse Reference Grossmann and Lohse2011). Despite much effort made in the search for the ultimate state, and reports for evidence of it, debates still continue regarding its existence. One way to achieve the ultimate state is to remove the BL in what is called homogeneous convection, which was first demonstrated numerically by Lohse & Toschi (Reference Lohse and Toschi2003), and later experimentally by Gibert et al. (Reference Gibert, Pabiou, Chillà and Castaing2006). In both cases a
$1/2$
state is now called the asymptotic ultimate state (Grossmann & Lohse Reference Grossmann and Lohse2011). Despite much effort made in the search for the ultimate state, and reports for evidence of it, debates still continue regarding its existence. One way to achieve the ultimate state is to remove the BL in what is called homogeneous convection, which was first demonstrated numerically by Lohse & Toschi (Reference Lohse and Toschi2003), and later experimentally by Gibert et al. (Reference Gibert, Pabiou, Chillà and Castaing2006). In both cases a
 $Nu\sim Ra^{1/2}$
was observed. A different approach is to retain the BLs, but add roughness to the surface of the top and bottom plates of the convection cell. The idea is that the roughness may help to trigger a transition to a turbulent BL at a lower
$Nu\sim Ra^{1/2}$
was observed. A different approach is to retain the BLs, but add roughness to the surface of the top and bottom plates of the convection cell. The idea is that the roughness may help to trigger a transition to a turbulent BL at a lower
 $Ra$
. Indeed, the value
$Ra$
. Indeed, the value
 $\unicode[STIX]{x1D6FD}=1/2$
has been obtained in experiments (Roche et al.
Reference Roche, Castaing, Chabaud and Hébral2001; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011; Xie & Xia Reference Xie and Xia2017). But direct numerical simulations (DNSs) of RB convection with rough surfaces in two dimensions found that
$\unicode[STIX]{x1D6FD}=1/2$
has been obtained in experiments (Roche et al.
Reference Roche, Castaing, Chabaud and Hébral2001; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011; Xie & Xia Reference Xie and Xia2017). But direct numerical simulations (DNSs) of RB convection with rough surfaces in two dimensions found that
 $\unicode[STIX]{x1D6FD}$
will fall back from
$\unicode[STIX]{x1D6FD}$
will fall back from
 $1/2$
to
$1/2$
to
 $1/3$
(the so-called classical scaling) when
$1/3$
(the so-called classical scaling) when
 $Ra$
becomes even higher (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). This suggests that the observed
$Ra$
becomes even higher (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). This suggests that the observed
 $1/2$
scaling is not related to the ultimate state that should survive at arbitrarily high
$1/2$
scaling is not related to the ultimate state that should survive at arbitrarily high
 $Ra$
once the system reached that state.
$Ra$
once the system reached that state.
2 Overview
Studying the effect of surface roughness in turbulent thermal convection is not new. The experiment by Shen, Tong & Xia (Reference Shen, Tong and Xia1996) was perhaps the first such study in the context of RB convection. This is followed by experiments made by Ciliberto & Laroche (Reference Ciliberto and Laroche1999), Du & Tong (Reference Du and Tong2000), Roche et al. (Reference Roche, Castaing, Chabaud and Hébral2001) and Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005). In these early studies, a general finding is that heat transport is enhanced once the thermal BL thickness becomes thinner than the roughness height; whether the scaling exponent $\unicode[STIX]{x1D6FD}$
changes or not depends on the details of the rough plates (for a brief review on these earlier studies, see, for example, Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014)).
$\unicode[STIX]{x1D6FD}$
changes or not depends on the details of the rough plates (for a brief review on these earlier studies, see, for example, Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014)).
According to the Grossmann–Lohse theory, the kinetic energy and thermal variance dissipation rates can be split into contributions from the bulk and the BLs, and when the dissipation is bulk-dominated $Nu\sim Ra^{1/2}$
asymptotically, whereas when BLs become dominant
$Nu\sim Ra^{1/2}$
asymptotically, whereas when BLs become dominant
 $Nu\sim Ra^{1/3}$
, again asymptotically (Grossmann & Lohse Reference Grossmann and Lohse2000). So, by perturbing the BL with surface roughness, one can reduce the BL contribution in the total dissipation and therefore change the overall heat transport to a more bulk-dominated behaviour. Based on this idea, Xie & Xia (Reference Xie and Xia2017) investigated experimentally using a series of convection cells with varying roughness topographies, which would introduce varying levels of BL perturbation. Indeed, they found that the value of
$Nu\sim Ra^{1/3}$
, again asymptotically (Grossmann & Lohse Reference Grossmann and Lohse2000). So, by perturbing the BL with surface roughness, one can reduce the BL contribution in the total dissipation and therefore change the overall heat transport to a more bulk-dominated behaviour. Based on this idea, Xie & Xia (Reference Xie and Xia2017) investigated experimentally using a series of convection cells with varying roughness topographies, which would introduce varying levels of BL perturbation. Indeed, they found that the value of
 $\unicode[STIX]{x1D6FD}$
can be tuned by the roughness topography. They further identified two scaling regimes in the heat-transport-enhanced regime, termed as regime II (corresponding to the thermal BL becoming submerged below the roughness height) and regime III (even the viscous BL becoming submerged; in contrast, regime I corresponds to both BLs being above the roughness height). By defining a roughness parameter
$\unicode[STIX]{x1D6FD}$
can be tuned by the roughness topography. They further identified two scaling regimes in the heat-transport-enhanced regime, termed as regime II (corresponding to the thermal BL becoming submerged below the roughness height) and regime III (even the viscous BL becoming submerged; in contrast, regime I corresponds to both BLs being above the roughness height). By defining a roughness parameter
 $\unicode[STIX]{x1D706}$
, i.e. the aspect ratio of the roughness elements, they showed that when
$\unicode[STIX]{x1D706}$
, i.e. the aspect ratio of the roughness elements, they showed that when
 $\unicode[STIX]{x1D706}$
changed from 0.5 to 4, the corresponding value of
$\unicode[STIX]{x1D706}$
changed from 0.5 to 4, the corresponding value of
 $\unicode[STIX]{x1D6FD}$
in regime II (a transient regime) changed from 0.36 to 0.59, and it changed from 0.3 to 0.5 in regime III (see, for example, figure 1(a) for the case with
$\unicode[STIX]{x1D6FD}$
in regime II (a transient regime) changed from 0.36 to 0.59, and it changed from 0.3 to 0.5 in regime III (see, for example, figure 1(a) for the case with
 $\unicode[STIX]{x1D706}=4.0$
). As
$\unicode[STIX]{x1D706}=4.0$
). As
 $Ra$
of the experiment is well below that at which one would expect to see the ultimate state, the observed
$Ra$
of the experiment is well below that at which one would expect to see the ultimate state, the observed
 $Nu\sim Ra^{1/2}$
scaling is clearly not related to the asymptotic state. Rather, this study demonstrates that one can tune the roughness topography to obtain a desired value of
$Nu\sim Ra^{1/2}$
scaling is clearly not related to the asymptotic state. Rather, this study demonstrates that one can tune the roughness topography to obtain a desired value of
 $\unicode[STIX]{x1D6FD}$
. The
$\unicode[STIX]{x1D6FD}$
. The
 $1/2$
scaling has also be obtained in 2-D DNS studies by Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) and Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017). While in the former the authors believe their results evidence a transition to the ultimate state, in the latter the authors demonstrate, surprisingly, that at even higher
$1/2$
scaling has also be obtained in 2-D DNS studies by Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) and Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017). While in the former the authors believe their results evidence a transition to the ultimate state, in the latter the authors demonstrate, surprisingly, that at even higher
 $Ra$
, the scaling exponent will fall back to the classical
$Ra$
, the scaling exponent will fall back to the classical
 $1/3$
scaling (figure 1
b), which implies that the observed
$1/3$
scaling (figure 1
b), which implies that the observed
 $1/2$
scaling should not be related to the ultimate state.
$1/2$
scaling should not be related to the ultimate state.
Figure 1. Here $Nu$
versus
$Nu$
versus
 $Ra$
with smooth and rough boundaries. (a) Three-dimensional (3-D) experiments (Xie & Xia Reference Xie and Xia2017) and (b) two-dimensional (2-D) DNS (Zhu et al.
Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019). The solid lines are power-law fits to the respective data sets.
$Ra$
with smooth and rough boundaries. (a) Three-dimensional (3-D) experiments (Xie & Xia Reference Xie and Xia2017) and (b) two-dimensional (2-D) DNS (Zhu et al.
Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019). The solid lines are power-law fits to the respective data sets.
By taking a different route than many of the previous studies that use monoscale roughness, Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) adopted a multiscale roughness topography in their simulation. By doing so, they find a $1/2$
scaling over three decades of
$1/2$
scaling over three decades of
 $Ra$
from
$Ra$
from
 $1\times 10^{8}$
to
$1\times 10^{8}$
to
 $1\times 10^{11}$
(figure 1
b). They show that the thermal BL is protruded by the three roughness heights sequentially (see the title image): at small
$1\times 10^{11}$
(figure 1
b). They show that the thermal BL is protruded by the three roughness heights sequentially (see the title image): at small
 $Ra$
, all the roughness elements are submerged inside the thermal BL; with increasing
$Ra$
, all the roughness elements are submerged inside the thermal BL; with increasing
 $Ra$
, part of the roughness elements protrude the thermal BL, with the smaller roughness still being submerged in the thermal BL; at the largest
$Ra$
, part of the roughness elements protrude the thermal BL, with the smaller roughness still being submerged in the thermal BL; at the largest
 $Ra$
, the thermal BL follows the surface roughness, acting as a effective smooth surface, resulting in the classical
$Ra$
, the thermal BL follows the surface roughness, acting as a effective smooth surface, resulting in the classical
 $1/3$
scaling (figure 1
b). This represents a new approach to perturb the BL in controlling heat transport scaling. In the simulation by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019), a three-level fractal-like structure was used, but in principle the level of scales is only limited by computational resources. One may then obtain a wider range of a
$1/3$
scaling (figure 1
b). This represents a new approach to perturb the BL in controlling heat transport scaling. In the simulation by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019), a three-level fractal-like structure was used, but in principle the level of scales is only limited by computational resources. One may then obtain a wider range of a
 $1/2$
scaling with a hierarchy of roughness scales. A similar approach can be taken for other scaling exponents (for example, with different values of
$1/2$
scaling with a hierarchy of roughness scales. A similar approach can be taken for other scaling exponents (for example, with different values of
 $\unicode[STIX]{x1D706}$
and multiscale roughness), making it possible to ‘design’ thermal convection systems with specific heat transport scalings.
$\unicode[STIX]{x1D706}$
and multiscale roughness), making it possible to ‘design’ thermal convection systems with specific heat transport scalings.
3 Future
Although both experimental and DNS studies show convincingly that the heat transport in turbulent convection can be tuned by manipulating the boundary layer topographies, there are differences between the 3-D experiments and 2-D simulations. The falling-back of $\unicode[STIX]{x1D6FD}$
from
$\unicode[STIX]{x1D6FD}$
from
 $1/2$
to the classical value of
$1/2$
to the classical value of
 $1/3$
for
$1/3$
for
 $Ra>2\times 10^{9}$
observed by Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) is not seen in experiments up to
$Ra>2\times 10^{9}$
observed by Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) is not seen in experiments up to
 $Ra\approx 1\times 10^{11}$
(Xie & Xia Reference Xie and Xia2017). Therefore, experimental studies with
$Ra\approx 1\times 10^{11}$
(Xie & Xia Reference Xie and Xia2017). Therefore, experimental studies with
 $Ra$
larger than
$Ra$
larger than
 $1\times 10^{11}$
will be needed to complete the picture. The physical mechanism leading to the observed relation between
$1\times 10^{11}$
will be needed to complete the picture. The physical mechanism leading to the observed relation between
 $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
 $\unicode[STIX]{x1D706}$
is not fully understood. To this end, studies on the spatial distribution of the energy dissipation rate and the thermal dissipation rate for different roughness configurations should provide some insight, which can only be done with realistic prospects using 3-D DNS. Moreover, the Prandtl number
$\unicode[STIX]{x1D706}$
is not fully understood. To this end, studies on the spatial distribution of the energy dissipation rate and the thermal dissipation rate for different roughness configurations should provide some insight, which can only be done with realistic prospects using 3-D DNS. Moreover, the Prandtl number
 $Pr$
, which characterises the relative thickness of the thermal BL to the viscous BL, is found to have a large impact on the heat transport in rough surface cells (Xie & Xia Reference Xie and Xia2017). Studies with a wider range of
$Pr$
, which characterises the relative thickness of the thermal BL to the viscous BL, is found to have a large impact on the heat transport in rough surface cells (Xie & Xia Reference Xie and Xia2017). Studies with a wider range of
 $Pr$
will thus complement our understanding of turbulent convection over rough surfaces. Finally, a crucial step towards real applications is the experimental realisation of the observations by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) in turbulent convection with multiscale roughness. With their tuning method, it is possible to design systems with desired heat transport efficiencies, which should find many practical applications.
$Pr$
will thus complement our understanding of turbulent convection over rough surfaces. Finally, a crucial step towards real applications is the experimental realisation of the observations by Zhu et al. (Reference Zhu, Stevens, Shishkina, Verzicco and Lohse2019) in turbulent convection with multiscale roughness. With their tuning method, it is possible to design systems with desired heat transport efficiencies, which should find many practical applications.