12 results
On the Schertz Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 837-845
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Siegel families with application to class fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 27 June 2018, pp. 751-771
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Construction of ray-class fields by smaller generators and their applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 781-812
- Print publication:
- August 2017
-
- Article
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On some Fricke families and application to the Lang–Schertz conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 18 May 2016, pp. 723-740
- Print publication:
- August 2016
-
- Article
- Export citation
Some applications of eta-quotients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 565-578
- Print publication:
- June 2016
-
- Article
- Export citation
Some applications of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 03 June 2015, pp. 91-106
-
- Article
- Export citation
Algebraic integers as special values of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 167-179
-
- Article
-
- You have access
- Export citation
On the genus of some modular curves of level N
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 54 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-297
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
genus theory for function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-310
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
On holomorphic differentials of some algebraic function field of one variable over C
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 43 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-405
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation



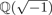
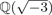
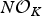
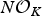
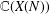
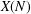
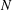
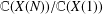
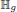 .
.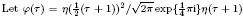 , where
, where 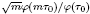 is an algebraic integer dividing
is an algebraic integer dividing 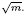 This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when
This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when 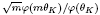 is a unit.
is a unit.