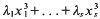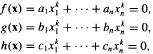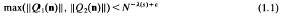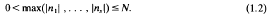15 results
RATIONAL POINTS ON THE INNER PRODUCT CONE VIA THE HYPERBOLA METHOD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 780-796
- Print publication:
- 2017
-
- Article
- Export citation
Sums of smooth squares
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1401-1441
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Additive representation in short intervals, I: Waring's problem for cubes
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1197-1220
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
Additive representation in thin sequences, VI: representing primes, and related problems
-
- Journal:
- Glasgow Mathematical Journal / Volume 44 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 26 February 2003, pp. 419-434
- Print publication:
- September 2002
-
- Article
-
- You have access
- Export citation
ON ARTIN'S CONJECTURE, II: PAIRS OF ADDITIVE FORMS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 84 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 29 April 2002, pp. 513-538
- Print publication:
- May 2002
-
- Article
- Export citation
Additive representation in thin sequences, II: The binary Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-125
- Print publication:
- December 2000
-
- Article
- Export citation
On smooth gaps between consecutive prime numbers
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-75
- Print publication:
- June 1999
-
- Article
- Export citation
ON ARTIN'S CONJECTURE, I: SYSTEMS OF DIAGONAL FORMS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 31 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 305-313
- Print publication:
- May 1999
-
- Article
- Export citation
4 - The Values of Binary Linear Forms at Prime Arguments
-
-
- Book:
- Sieve Methods, Exponential Sums, and their Applications in Number Theory
- Published online:
- 03 February 2010
- Print publication:
- 30 January 1997, pp 87-100
-
- Chapter
- Export citation
Cubic Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-277
- Print publication:
- December 1995
-
- Article
- Export citation
On sums of two squarefull numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 116 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
- Print publication:
- July 1994
-
- Article
- Export citation
Three additive congruences to a large prime modulus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-368
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
Pairs of quadratic forms modulo one
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 51-61
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Simultaneous additive congruences to a large prime modulus
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1992
-
- Article
- Export citation
On pairs of cubic Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 250-263
- Print publication:
- December 1991
-
- Article
- Export citation