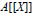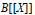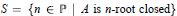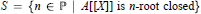32 results
Biotic and Abiotic Forcing During the Transition to Modern Grassland Ecosystems: Evolutionary and Ecological Responses of Small Mammal Communities Over the Last 5 Million Years
-
- Journal:
- The Paleontological Society Papers / Volume 21 / October 2015
- Published online by Cambridge University Press:
- 21 July 2017, pp. 197-218
- Print publication:
- October 2015
-
- Article
- Export citation
On the Prime Ideals in a Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-319
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
On zero-dimensionality and fragmented rings
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 60 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-151
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Root Closure in Integral Domains, III
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-9
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
Weak Normalization of Power Series Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-433
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
On t- Spec(R[[X]])
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 2 / 01 June 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 187-195
- Print publication:
- 01 June 1995
-
- Article
-
- You have access
- Export citation
Hilbert Rings Arising as Pullbacks
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 4 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 431-438
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation
The expected dimension of a sum of vector subspaces
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 45 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-477
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
On n-flat modules over a commutative ring
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 43 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 17 April 2009, pp. 491-498
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Nearly integral homomorphisms of commutative rings
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 40 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-12
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Pairs of Rings with the Same Prime Ideals, II
-
- Journal:
- Canadian Journal of Mathematics / Volume 40 / Issue 6 / 01 December 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1399-1409
- Print publication:
- 01 December 1988
-
- Article
-
- You have access
- Export citation
Integrally closed factor domains
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 37 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-366
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
Seminormal rings generated by algebraic integers
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-154
- Print publication:
- December 1987
-
- Article
- Export citation
Going-down underrings
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 36 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 17 April 2009, pp. 503-513
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
On the Criteria of D.D. Anderson for Invertible and Flat Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 1 / 01 March 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 25-32
- Print publication:
- 01 March 1986
-
- Article
-
- You have access
- Export citation
Integrally Closed Condensed Domains are Bézout
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 1 / 01 March 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-102
- Print publication:
- 01 March 1985
-
- Article
-
- You have access
- Export citation
On Chain Conditions in Integral Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 3 / 01 September 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 351-359
- Print publication:
- 01 September 1984
-
- Article
-
- You have access
- Export citation
Universally Incomparable Ring-Homomorphisms
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 29 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-302
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
On the Product of Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 1 / 01 March 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-114
- Print publication:
- 01 March 1983
-
- Article
-
- You have access
- Export citation
Lying-Over Pairs of Commutative Rings
-
- Journal:
- Canadian Journal of Mathematics / Volume 33 / Issue 2 / 01 April 1981
- Published online by Cambridge University Press:
- 20 November 2018, pp. 454-475
- Print publication:
- 01 April 1981
-
- Article
-
- You have access
- Export citation