15 results
A new proof of Halász’s theorem, and its consequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 126-163
- Print publication:
- January 2019
-
- Article
-
- You have access
- HTML
- Export citation
WHEN DOES THE BOMBIERI–VINOGRADOV THEOREM HOLD FOR A GIVEN MULTIPLICATIVE FUNCTION?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 24 August 2018, e15
-
- Article
-
- You have access
- Open access
- Export citation
SMOOTH-SUPPORTED MULTIPLICATIVE FUNCTIONS IN ARITHMETIC PROGRESSIONS BEYOND THE
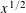 $x^{1/2}$-BARRIER
$x^{1/2}$-BARRIER
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 895-918
- Print publication:
- 2017
-
- Article
- Export citation
BIG BIASES AMONGST PRODUCTS OF TWO PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 502-507
- Print publication:
- 2016
-
- Article
- Export citation
Close Lattice Points on Circles
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1214-1238
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
Irreducibility and greatest common divisor algorithms for sparse polynomials
-
-
- Book:
- Number Theory and Polynomials
- Published online:
- 04 May 2010
- Print publication:
- 08 May 2008, pp 155-176
-
- Chapter
- Export citation
Decay of Mean Values of Multiplicative Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 6 / 01 December 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1191-1230
- Print publication:
- 01 December 2003
-
- Article
-
- You have access
- Export citation
The Number of Fields Generated by the Square Root of Values of a Given Polynomial
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 1 / 01 March 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-79
- Print publication:
- 01 March 2003
-
- Article
-
- You have access
- Export citation
UNIT FRACTIONS AND THE CLASS NUMBER OF A CYCLOTOMIC FIELD
-
- Journal:
- Journal of the London Mathematical Society / Volume 66 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 24 March 2003, pp. 579-591
- Print publication:
- December 2002
-
- Article
- Export citation
An Upper Bound on the Least Inert Prime in a Real Quadratic Field
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 2 / 01 April 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-380
- Print publication:
- 01 April 2000
-
- Article
-
- You have access
- Export citation
On the scarcity of powerful binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-410
- Print publication:
- December 1999
-
- Article
- Export citation
7 - A Decomposition of Riemann's Zeta-Function
-
-
- Book:
- Analytic Number Theory
- Published online:
- 08 April 2010
- Print publication:
- 16 October 1997, pp 95-102
-
- Chapter
- Export citation
Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-107
- Print publication:
- June 1996
-
- Article
- Export citation
A Note on Sums of Primes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 4 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-454
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation
Refining the conditions on the Fermat quotient
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 98 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-8
- Print publication:
- July 1985
-
- Article
- Export citation



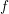
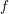
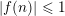
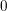
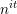
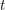
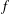
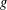
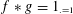
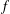
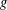
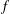
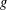
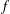
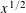
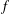
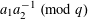

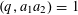
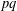

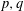
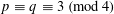
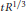
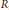
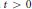
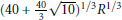
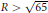
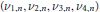
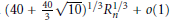
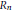
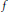
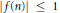

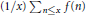
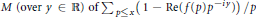
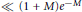


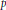
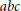
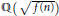
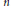
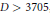
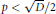
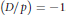
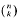 with 3≤
with 3≤ . Unconditionally, it is shown that there are
. Unconditionally, it is shown that there are 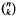 must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently
must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 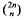 is not squarefree once
is not squarefree once 
