Article contents
An Upper Bound on the Least Inert Prime in a Real Quadratic Field
Published online by Cambridge University Press: 20 November 2018
Abstract
It is shown by a combination of analytic and computational techniques that for any positive fundamental discriminant 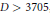 $D\,>\,3705$, there is always at least one prime
$D\,>\,3705$, there is always at least one prime 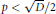 $p\,<\,\sqrt{D}/2$ such that the Kronecker symbol
$p\,<\,\sqrt{D}/2$ such that the Kronecker symbol 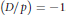 $(D/P)\,=\,-1$.
$(D/P)\,=\,-1$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 5
- Cited by


