In this paper we give a characterisation of -invariant real hypersurfaces of type A; that is, a tube over a totally geodesic G2(ℂm+1) in complex two-plane Grassmannians G2(ℂm+2) or a ruled real hypersurface foliated by complex hypersurfaces which includes a maximal totally geodesic submanifold G2(ℂm+1) in G2(ℂm+2) in terms of η-parallel shape operator.

We show that the inverse limit of any inverse sequence of compact metric spaces and surjective bonding maps is in fact the limit of a sequence of homeomorphic copies of the same spaces with respect to the Hausdorff metric.

Let R be a finite ring. Let us denote its group of units by G = G(R) and its Jacobson radical by J = J(R). Let n be an arbitrary integer. We prove that R is an n-insertive ring if and only if G is an n-insertive group and show that every n-insertive finite ring is a direct sum of local rings. We prove that if n is a unit, then the local ring R is n-insertive if and only if its Jacobson group 1 + J is n-insertive and find an example to show that this is not true if n is a non-unit.

In this note we analyse the analogy between m-potent and p-central restricted Lie algebras and p-groups. For restricted Lie algebras the notion of m-potency has stronger implications than for p-groups (Theorem A). Every finite-dimensional restricted Lie algebra  is isomorphic to for some finite-dimensional p-central restricted Lie algebra (Proposition B). In particular, for restricted Lie algebras there does not hold an analogue of J.Buckley's theorem. For p odd one can characterise powerful restricted Lie algebras in terms of the cup product map in the same way as for finite p-groups (Theorem C). Moreover, the p-centrality of the finite-dimensional restricted Lie algebra  has a strong implication on the structure of the cohomology ring H•(,) (Theorem D).

The object of this paper is to develop and study group theoretic analogues of some of the fundamental concepts and results of arithmetic functions of positive integers.

In this paper, a new type of generalised convexity—semilocal E-convexity is introduced by combining the concepts of the semi-E-convexity in X.S. Chen [J. Math. Anal. Appl. 275(2002), 251–262] and semilocal convexity in G.M. Ewing [SIAM. Rev. 19(1977), 202–220], and some of its basic characters are discussed. By utilising the new concepts, we derive some optimality conditions and establish some duality results for the inequality constrained optimisation problem.

For a knot K in a homology 3-sphere Σ, by Σ(K;p/q), we denote the resulting 3-manifold of p/q-surgery along K. We say that the manifold or the surgery is of lens type if Σ(K;p/q) has the same Reidemeister torsion as a lens space.

We prove that, for Σ(K;p/q) to be of lens type, it is a necessary and sufficient condition that the Alexander polynomial ΔK(t) of K is equal to that of an (i, j)-torus knot T(i, j) modulo (tp – 1).

We also deduce two results: If Σ(K;p/q) has the same Reidemeister torsion as L(p, q') then (1) 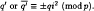(2) The multiple of ΣK(tk) over k ∈ (i) is ±tm modulo (tp – 1), where (i) is the subgroup in (Z/pZ)×/{±1} generated by i. Conversely, if a subgroup H of (Z/pZ)×/{±l} satisfying that the product of ΣK(tk) (k ∈ H) is ±tm modulo (tp – 1), then H includes i or j.

Here, i, j are the parameters of the torus knot above.

Let K be a number field. An element b ∈ K* being given, let Cb be the curve defined over K by the equation x4 + y4 = bz4. Let Cb(K) be the set of the K-rational points of Cb. This paper uses Dem'janenko and Manin type methods to obtain effective criteria for Cb(K) to be empty.

In one of their most recent works, George Andrews and Peter Paule continue their study of partition functions via MacMahon's Partition Analysis by considering partition functions associated with directed graphs which consist of chains of hexagons. In the process, they prove a congruence related to one of these partition functions and conjecture a number of similar congruence results. Our first goal in this note is to reprove this congruence by explicitly finding the generating function in question. We then prove one of the conjectures posed by Andrews and Paule as well as a number of congruences not mentioned by them. All of our results follow from straightforward generating function manipulations.

Let τ be a hereditary torsion theory in R-Mod. Then any ring homomorphism γ: R → S induces in S-Mod a torsion theory σ given by the condition that a left S-module is σ-torsion if and only if it is τ-torsion as a left R-module. We show that if γ: R → S is a ring epimorphism and A is a τ-injective left R-module, then AnnA Ker(γ) is σ-injective as a left S-module. As a consequence, we relate τ-injectivity and σ-injectivity, and we give some applications.

Let p ≥ 5 be a prime and for a, b ε p, let Ea, b denote the elliptic curve over p with equation y2 = x3 + ax + b. As usual define the trace of Frobenius ap, a, b by

We use elementary facts about exponential sums and known results about binary quadratic forms over finite fields to evaluate the sums and for primes p in various congruence classes.

As an example of our results, we prove the following: Let p ≡ 5 (mod 6) be prime and let b ε *p. Then