We obtain an optimal actuation waveform for fast synchronization of periodic airfoil wakes through the phase reduction approach. Using the phase reduction approach for periodic wake flows, the spatial sensitivity fields with respect to the phase of the vortex shedding are obtained. The phase sensitivity fields can uncover the synchronization properties in the presence of periodic actuation. This study seeks a periodic actuation waveform using phase-based analysis to minimize the time for synchronization to modify the wake shedding frequency of NACA0012 airfoil wakes. This fast synchronization waveform is obtained theoretically from the phase sensitivity function by casting an optimization problem. The obtained optimal actuation waveform becomes increasingly non-sinusoidal for higher angles of attack. Actuation based on the obtained waveform achieves rapid synchronization within as low as two vortex shedding cycles irrespective of the forcing frequency, whereas traditional sinusoidal actuation requires ${O}(10)$ shedding cycles. Further, we analyse the influence of actuation frequency on the vortex shedding and the aerodynamic coefficients using force-element analysis. The present analysis provides an efficient way to modify the vortex lock-on properties in a transient manner with applications to fluid–structure interactions and unsteady flow control.

Two-dimensional horizontally periodic Rayleigh–Bénard convection between stress-free boundaries displays two distinct types of states, depending on the initial conditions. Roll states are composed of pairs of counter-rotating convection rolls. Windy states are dominated by strong horizontal wind (also called zonal flow) that is vertically sheared, precludes convection rolls and suppresses heat transport. Windy states occur only when the Rayleigh number $Ra$ is sufficiently above the onset of convection. At intermediate $Ra$ values, windy states can be induced by suitable initial conditions, but they undergo a transition to roll states after finite lifetimes. At larger $Ra$ values, where windy states have been observed for the full duration of simulations, it is unknown whether they represent chaotic attractors or only metastable states that would eventually undergo a transition to roll states. We study this question using direct numerical simulations of a fluid with a Prandtl number of 10 in a layer whose horizontal period is eight times its height. At each of seven $Ra$ values between $9\times 10^6$ and $2.25\times 10^7$ we have carried out 200 or more simulations, all from initial conditions leading to windy convection with finite lifetimes. The lifetime statistics at each $Ra$ indicate a memoryless process with survival probability decreasing exponentially in time. The mean lifetimes grow with $Ra$ approximately as $Ra^4$. This analysis provides no $Ra$ value at which windy convection becomes stable; it might remain metastable at larger $Ra$ with extremely long lifetimes.

This work investigates the statistical response of short and long laminar separation bubbles to external flow parameters, such as Reynolds number, free-stream turbulence intensity and streamwise pressure gradient, known to govern bubble formation and characteristics. A parametric experimental campaign has been performed using particle image velocimetry on a flat plate to provide a comprehensive database for the characterization of separation-induced transition in both short and long separation bubbles. The proper orthogonal decomposition (POD) was applied to the data set of all dividing streamlines commonly used to identify a laminar separation bubble. This provides an optimal state-space basis for the data-driven classification of the state of a laminar separation bubble, with the leading modes capturing the change in length and height of the laminar separation bubble in response to changes in the flow parameters. When projected onto the POD subspace constituted by the first three leading modes, the normalized data from the present study and the results from prior investigations not used in the modal analysis collapse on the same trajectory in the low-dimensional space. The present POD basis can be therefore adopted for the description of the general response of the time-mean shape of a laminar separation bubble to changes in the main influencing parameters. A well-defined pattern was observed in the case of short laminar separation bubbles in the reduced-order space defined by the first three POD coefficients, whereas a higher dispersion in the long-bubble regime indicates an increased sensitivity of long bubbles to the external flow characteristics.

‘Storm oil’ – nearly water-insoluble oil poured into the ocean and acting as a surfactant – has been used since ancient times to smooth the waves on the ocean. It was first scientifically described by Benjamin Franklin (Phil. Trans. R. Soc. Lond., vol. 64, 1774, pp. 445–460). In a recent paper, by combining highly controlled experiments in a wave tank and direct numerical simulations, Erinin et al. (J. Fluid Mech., vol. 972, 2023, R5) have now beautifully revealed the strong effect of soluble surfactants on the dynamics of plunging breakers. Remarkably, it is not the change in surface tension which mainly matters, but the surface tension gradient which emerges through compression and dilation of the plunging breaker surface.

Fluid flow passing a post-buckled sheet placed between two close confining walls induces periodic snap-through oscillations and contacts that can be employed for triboelectric energy harvesting. The responses of a two-dimensional sheet to a uniform flow and wall confinement in both equilibrium and post-equilibrium states are numerically investigated by varying the distance between the two ends of the sheet, gap distance between the confining walls and flow velocity. Cases with strong interactions between the sheet and walls are of most interest for examining how contact with the walls affects the dynamics of the sheet and flow structure. At equilibrium, contact with the wall displaces the sheet to form a nadir on its front part, yielding a lower critical flow velocity for the transition to snap-through oscillations. However, reducing the gap distance between the walls below a certain threshold distinctly shifts the shape of the sheet, alters the pressure distribution and eventually leads to a notable delay in the instability. The contact between the oscillating sheet and the walls at post-equilibrium is divided into several distinct modes, changing from sliding/rolling contact to bouncing contact with increasing flow velocity. During this transition, the time-averaged contact force exerted on the sheet decreases with the flow velocity. The vortices generated at the extrema of the oscillating sheet are annihilated by direct contact with the walls and merging with the shear layers formed by the walls, resulting in a wake structure dominated by the unstable shear layers.

We use direct numerical simulation to study the vibroacoustic response of an elastic plate in a turbulent channel at $Re_\tau$ of 180 and 400 for three plate boundary conditions and two materials – synthetic rubber and stainless steel. The fluid–structure–acoustic coupling is assumed to be one-way coupled, i.e. the fluid affects the solid and not vice versa, and the solid affects the acoustic medium and not vice versa. The wall pressure consists of intermittent large-amplitude fluctuations associated with the near-wall, burst-sweep cycle of events. For stainless steel plates, displacement has similar large-amplitude peak events due to comparable time scales of plate vibration and near-wall eddies. For synthetic rubber plates, large-amplitude displacement fluctuations are observed only near clamped or simply supported boundaries. Away from boundaries, plate displacement resembles an amplitude-modulated wave, and no large-amplitude events are observed. We discuss displacement and acoustic pressure spectra over different frequency ranges. For frequencies much smaller than the first natural frequency, the product of plate-averaged displacement spectrum and bending stiffness squared collapses with Reynolds number and plate material in outer units. At high frequencies, displacement and acoustic pressure spectra scale better in inner units, and the scaling depends on the type of damping. For synthetic rubber plates, the spectra display an overlap region that collapses in both outer and inner units. Soft plate deformation displays a range of length scales. However, stiff plate deformation does not exhibit a similar range of scales and resembles plate mode shapes. The soft plate has two distinct deformation structures. Low-speed, large deformation structures with slow formation/break-up time scales are found away from boundaries. High-speed, small deformation structures with fast formation/break-up time scales formed due to boundary reflections exist near the boundaries.

A linear stability analysis of circular Couette flow of a Bingham fluid subjected to axisymmetric perturbations was presented by Peng & Zhu (J. Fluid Mech., vol. 512, 2004, pp. 21–45) and Landry et al. (J. Fluid Mech., vol. 560, 2006, pp. 321–353). Here, we consider the stability of this flow with respect to a finite amplitude perturbation. We focus particularly on the case where the basic flow has an unyielded fluid layer on outer cylinder. A weakly nonlinear stability analysis is developed for a wide gap and a narrow gap. A third-order Ginzburg–Landau equation is derived, and the influence of the different nonlinearities on bifurcation features is investigated in detail. The results indicate that: (i) the nonlinear inertial terms act in favour of pitchfork supercritical bifurcation and the nonlinear yield stress terms promote a subcritical bifurcation; (ii) for a range of Bingham numbers $B$, the extent of which depends on the radius ratio and outer Reynolds number, the nonlinear yield stress terms are dominant and the primary bifurcation is subcritical. The amplitude analysis indicates that in the supercritical bifurcation regime, near the threshold, when the nonlinear inertial terms are dominant, the amplitude decreases slightly with increasing $B$. Once the nonlinear yield stress terms start to become significant, the equilibrium amplitude increases substantially with increasing $B$. Similar trends are observed for Taylor vortex strength. Finally, the erosion of the static layer is analysed. It is shown that the nonlinear yield stress terms play a significant role.

The scaling law for the horizontal length scale $\ell$ relative to the domain height $L$, originating from the linear theory of quasi-static magnetoconvection, $\ell /L \sim Q^{-1/6}$, has been verified through two-dimensional (2-D) direct numerical simulation (DNS), particularly at high values of the Chandrasekhar number ($Q$). This relationship remains valid within a specific flow regime characterized by columnar structures aligned with the magnetic field. Expanding upon the $Q$-dependence of the horizontal length scale, we have derived scaling laws for the Nusselt number ($Nu$) and the Reynolds number ($Re$) as functions of the driving forces (Rayleigh number ($Ra$) and $Q$) in quasi-static magnetoconvection influenced by a strong magnetic field. These scaling relations, $Nu \sim Ra/Q$ and $Re \sim Ra Q^{-5/6}$, have been successfully validated using 2-D DNS data spanning a wide range of five decades in $Q$, ranging from $10^5$ to $10^9$. The successful validation of the relations at large $Q$ values, combined with our theoretical analysis of dissipation rates and the incorporation of the horizontal length scale's influence on scaling behaviour, presents a valid approach for deriving scaling laws under various conditions.

We develop and analyse a continuum model of two-phase slurry dynamics for planetary cores. Mixed solid–liquid slurry regions may be ubiquitous in the upper cores of small terrestrial bodies and have also been invoked to explain anomalous seismic structure in the F-layer at the base of Earth's liquid iron core. These layers are expected to influence the dynamics and evolution of planetary cores, including their capacity to generate global magnetic fields; however, to date, models of two-phase regions in planetary cores have largely ignored the complex fluid dynamics that arises from interactions between phases. As an initial application of our model, and to focus on fundamental fluid dynamical processes, we consider a non-rotating and non-magnetic slurry comprised of a single chemical component with a temperature that is tied to the liquidus. We study one-dimensional solutions in a configuration set up to mimic Earth's F-layer, varying gravitational strength $R$, the solid/liquid viscosity ratio $\lambda _{\mu }$ and the interaction parameter $K$, which measures friction between the phases. We develop scalings describing behaviour in the limit $R \gg 1$ and $\lambda _{\mu } \gg 1$, which are in excellent agreement with our numerical results. Application to Earth's core, where $R \sim 10^{28}$ and $\lambda _{\mu } \sim 10^{22}$, suggests that a pure iron slurry F-layer would contain a mean solid fraction of at most 5 %.

While tapered swept wings are widely used, the influence of taper on their post-stall wake characteristics remains largely unexplored. To address this issue, we conduct an extensive study using direct numerical simulations to characterize the wing taper and sweep effects on laminar separated wakes. We analyse flows behind NACA 0015 cross-sectional profile wings at post-stall angles of attack $\alpha =14^\circ$–$22^\circ$ with taper ratios $\lambda =0.27$–$1$, leading-edge sweep angles $0^\circ$–$50^\circ$ and semi aspect ratios $sAR =1$ and $2$ at a mean-chord-based Reynolds number of $600$. Tapered wings have smaller tip chord length, which generates a weaker tip vortex, and attenuates inboard downwash. This results in the development of unsteadiness over a large portion of the wingspan at high angles of attack. For tapered wings with backward-swept leading edges, unsteadiness emerges near the wing tip. On the other hand, wings with forward-swept trailing edges are shown to concentrate wake-shedding structures near the wing root. For highly swept untapered wings, the wake is steady, while unsteady shedding vortices appear near the tip for tapered wings with high leading-edge sweep angles. For such wings, larger wake oscillations emerge near the root as the taper ratio decreases. While the combination of taper and sweep increases flow unsteadiness, we find that tapered swept wings have more enhanced aerodynamic performance than untapered and unswept wings, exhibiting higher time-averaged lift and lift-to-drag ratio. The current findings shed light on the fundamental aspects of flow separation over tapered wings in the absence of turbulent flow effects.

A thermodynamically consistent kinetic model is proposed for the non-equilibrium transport of confined van der Waals fluids, where the long-range molecular attraction is considered by a mean-field term in the transport equation, and the transport coefficients are tuned to match the experimental data. The equation of state of the van der Waals fluids can be obtained from an appropriate choice of the pair correlation function. By contrast, the modified Enskog theory predicts non-physical negative transport coefficients near the critical temperature and may not be able to recover the Boltzmann equation in the dilute limit. In addition, the shear viscosity and thermal conductivity are predicted more accurately by taking gas molecular attraction into account, while the softened Enskog formula for hard-sphere molecules performs better in predicting the bulk viscosity. The present kinetic model agrees with the Boltzmann model in the dilute limit and with the Navier–Stokes equations in the continuum limit, indicating its capability in modelling dilute-to-dense and continuum-to-non-equilibrium flows. The new model is examined thoroughly and validated by comparing it with the molecular dynamics simulation results. In contrast to the previous studies, our simulation results reveal the importance of molecular attraction even for high temperatures, which holds the molecules to the bulk while the hard-sphere model significantly overestimates the density near the wall. Because the long-range molecular attraction is considered appropriately in the present model, the velocity slip and temperature jump at the surface for the more realistic van der Waals fluids can be predicted accurately.

A light breeze rising over calm water initiates an intricate chain of events that culminates in a centimetres-deep turbulent shear layer capped by gravity–capillary ripples. At first, viscous stress accelerates a laminar wind-drift layer until small surface ripples appear. The surface ripples then catalyse the growth of a second instability in the wind-drift layer, which eventually sharpens into along-wind jets and downwelling plumes, before devolving into three-dimensional turbulence. In this paper, we compare laboratory experiments with simplified, wave-averaged numerical simulations of wind-drift layer evolution beneath monochromatic, constant-amplitude surface ripples seeded with random initial perturbations. Despite their simplicity, our simulations reproduce many aspects of the laboratory-based observations – including the growth, nonlinear development and turbulent breakdown the wave-catalysed instability – generally validating our wave-averaged model. But we also find that the simulated development of the wind-drift layer is disturbingly sensitive to the amplitude of the prescribed surface wave field, such that agreement is achieved through suspiciously careful tuning of the ripple amplitude. As a result of this sensitivity, we conclude that wave-averaged models should really describe the coupled evolution of the surface waves together with the flow beneath to be regarded as truly ‘predictive’.

The motion of a freely rotating prolate spheroid in a simple shear flow of a dilute polymeric solution is examined in the limit of large particle aspect ratio, 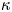$\kappa$. A regular perturbation expansion in the polymer concentration, 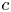$c$, a generalized reciprocal theorem, and slender body theory to represent the velocity field of a Newtonian fluid around the spheroid are used to obtain the 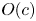$O(c)$ correction to the particle's orientational dynamics. The resulting dynamical system predicts a range of orientational behaviours qualitatively dependent upon 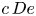$c\, De$ (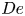$De$ is the imposed shear rate times the polymer relaxation time) and 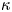$\kappa$ and quantitatively on 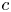$c$. At a small but finite 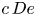$c\, De$, the particle spirals towards a limit cycle near the vorticity axis for all initial conditions. Upon increasing 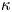$\kappa$, the limit cycle becomes smaller. Thus, ultimately the particle undergoes a periodic motion around and at a small angle from the vorticity axis. At moderate 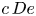$c\, De$, a particle starting near the flow–gradient plane departs it monotonically instead of spirally, as this plane (a limit cycle at smaller 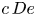$c\, De$) obtains a saddle and an unstable node. The former is close to the flow direction. Upon further increasing 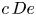$c\, De$, the saddle node changes to a stable node. Therefore, depending upon the initial condition, a particle may either approach a periodic orbit near the vorticity axis or obtain a stable orientation near the flow direction. Upon further increasing 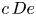$c\, De$, the limit cycle near the vorticity axis vanishes, and the particle aligns with the flow direction for all starting orientations.

We analytically derive an amplitude equation for the weakly nonlinear evolution of the linearly most amplified response of a non-normal dynamical system. The development generalizes the method proposed in Ducimetière et al. (J. Fluid Mech., vol. 947, 2022, A43), in that the base flow now arbitrarily depends on time, and the operator exponential formalism for the evolution of the perturbation is not used. Applied to the two-dimensional Lamb–Oseen vortex, the amplitude equation successfully predicts the nonlinearities to weaken or reinforce the transient gain in the weakly nonlinear regime. In particular, the minimum amplitude of the linear optimal initial perturbation required for the amplitude equation to lose a solution, interpreted as the flow experiencing a bypass (subcritical) transition, is found to decay as a power law with the Reynolds number. Although with a different exponent, this is recovered in direct numerical simulations, showing a transition towards a tripolar state. The simplicity of the amplitude equation and the link made with the sensitivity formula permits a physical interpretation of nonlinear effects, in light of existing work on Landau damping and on shear instabilities. The amplitude equation also quantifies the respective contributions of the second harmonic and the spatial mean flow distortion in the nonlinear modification of the gain.

We investigate experimentally and theoretically the interactions between a cavitation bubble and a hemispherical pendant oil droplet immersed in water. In experiments, the cavitation bubble is generated by a focused laser pulse right below the pendant droplet with well-controlled bubble–wall distances and bubble–droplet size ratios. By high-speed imaging, four typical interactions are observed, namely: oil droplet rupture; water droplet entrapment; oil droplet large deformation; and oil droplet mild deformation. The bubble jetting at the end of collapse and the migration of the bubble centroid are particularly different in each bubble–droplet interaction. We propose theoretical models based on the method of images for calculating the Kelvin impulse and the anisotropy parameter which quantitatively reflects the migration of the bubble centroid at the end of the collapse. Finally, we explain that a combination of the Weber number and the anisotropy parameter determines the regimes of the bubble–droplet interactions.

When inertial particles are dispersed in a turbulent flow at sufficiently high concentrations, the continuous and dispersed phases are two-way coupled. Here, we show via laboratory measurements how, as the suspended particles modify the turbulence, their behaviour is also profoundly changed. In particular, we investigate the spatial distribution and motion of sub-Kolmogorov particles falling in homogeneous air turbulence. We focus on the regime considered in Hassaini & Coletti (J. Fluid Mech., vol. 949, 2022, A30), where the turbulent kinetic energy and dissipation rate were found to increase as the particle volume fraction increases from $10^{-6}$ to $5\times 10^{-5}$. This leads to strong intensification of the clustering, encompassing a larger fraction of the particles and over a wider range of scales. The settling rate is approximately doubled over the considered range of concentrations, with particles in large clusters falling even faster. The settling enhancement is due in comparable measure to the predominantly downward fluid velocity at the particle location (attributed to the collective drag effect) and to the larger slip velocity between the particles and the fluid. With increasing loading, the particles become less able to respond to the fluid fluctuations, and the random uncorrelated component of their motion grows. Taken together, the results indicate that the concentrated particles possess an effectively higher Stokes number, which is a consequence of the amplified dissipation induced by two-way coupling. The larger relative velocities and accelerations due to the increased fall speed may have far-reaching consequences for the inter-particle collision probability.

While previous experimental and numerical studies of dilute microswimmer suspensions have focused on the behaviours of swimmers in the bulk flow and near boundaries, models typically do not account for the interplay between bulk flow and the choice of boundary conditions imposed in continuum models. In our work, we highlight the effect of boundary conditions on the bulk flow distributions, such as through the development of boundary layers or secondary peaks of cell accumulation in bulk-flow swimmer dynamics. For the case of a dilute swimmer suspension in Poiseuille flow, we compare the distribution (in physical and orientation space) obtained from individual-based stochastic models with those from continuum models, and identify under what conditions it is mathematically sensible to use specific continuum boundary conditions to capture different physical scenarios (i.e. specular reflection, uniform random reflection and absorbing boundaries). We identify that the spread of preferred cell orientations is dependent on the interplay between rotation driven by the shear flow (Jeffery orbits) and rotational diffusion. We find that in the absence of hydrodynamic wall interactions, swimmers preferentially approach the walls perpendicular to the surface in the presence of high rotational diffusion, and that the preferential approach of swimmers to the walls is shape-dependent at low rotational diffusion (when suspensions tend towards a fully deterministic case). In the latter case, the preferred orientations are nearly parallel to the surface for elongated swimmers and nearly perpendicular to the surface for near-spherical swimmers. Furthermore, we highlight the effects of swimmer geometries and shear throughout the bulk-flow on swimmer trajectories and show how the full history of bulk-flow dynamics affects the orientation distributions of microswimmer wall incidence.

The spatial relationship between turbulent and particle concentration structures is investigated based on the turbulent velocity and particle concentration data obtained synchronously at the Qingtu Lake Observation Array site. In addition to the observation of particle concentration structures that contain not only large-scale coherence but also significant energy in the high-Reynolds-number atmospheric surface layer (ASL), the scale of turbulent motions that have the most significant coherence with particle concentration is found to follow a 1/2 power scaling law with the local height and ASL thickness. Moreover, large-scale turbulent velocity fluctuations have a significant amplitude modulation effect on particle concentration fluctuations, but the modulating influence is different for small dust particles and large saltating particles. Based on the interphase amplitude modulation, there exists a particle–turbulence structure phase difference that varies with height, which further makes the structure inclination angle of the particle concentration larger than that of the turbulence. In this scenario, a conceptual model reflecting the relationship between the two is proposed, and a quantitative formulation is further derived and found to be in good agreement with the experimental results. These findings and the proposed model contribute insights into particle–turbulence interactions, thereby providing theoretical support for a unified model of turbulence dynamics and particle kinematics.

We study the emergence of fluid flow in a closed chamber that is driven by dynamical deformations of an elastic sheet. The sheet is compressed between the sidewalls of the chamber and partitions it into two separate parts, each of which is initially filled with an inviscid fluid. When fluid exchange is allowed between the two compartments of the chamber, the sheet becomes unstable, and its motion displaces the fluid from rest. We derive an analytical model that accounts for the coupled, two-way, fluid–sheet interaction. We show that the system depends on four dimensionless parameters: the normalized excess length of the sheet compared with the lateral dimension of the chamber, $\varDelta$; the normalized vertical dimension of the chamber; the normalized initial volume difference between the two parts of the chamber, $v_{du}(0)$; and the structure-to-fluid mass ratio, $\lambda$. We investigate the dynamics at the early times of the system's evolution and then at moderate times. We obtain the growth rates and the frequency of vibrations around the second and the first buckling modes, respectively. Analytical solutions are derived for these linear stability characteristics within the limit of the small-amplitude approximation. At moderate times, we investigate how the sheet escapes from the second mode. Given the chamber's dimensions, we show that the initial energy of the sheet is mostly converted into hydrodynamic energy of the fluid if $\lambda \ll 1$ and into kinetic energy of the sheet if $\lambda \gg 1$. In both cases, most of the initial potential energy is released at time $t_{p}\simeq \ln [c \varDelta ^{1/2}/v_{du}(0)]/\sigma$, where $\sigma$ is the growth rate and $c$ is a constant.

Dense granular systems that consist of particles of disparate sizes segregate based on size during flow, resulting in complex, coupled segregation and flow patterns. The ability to predict how granular mixtures segregate is important in the design of industrial processes and the understanding of geophysical phenomena. The two primary drivers of size segregation are pressure gradients and shear-strain-rate gradients. In this work, we isolate size segregation driven by shear-strain-rate gradients by studying two dense granular flow geometries with constant pressure fields: gravity-driven flow down a long vertical chute with rough parallel walls and annular shear flow with rough inner and outer walls. We perform discrete element method (DEM) simulations of dense flow of bidisperse granular systems in both flow geometries, while varying system parameters, such as the flow rate, flow configuration size, fraction of large/small grains and grain-size ratio, and use DEM data to inform continuum constitutive equations for the relative flux of large and small particles. When the resulting continuum model for the dynamics of size segregation is coupled with the non-local granular fluidity model – a non-local continuum model for dense granular flow rheology – we show that both flow fields and segregation dynamics may be simultaneously captured using this coupled, continuum system of equations.