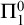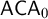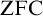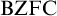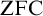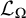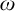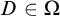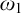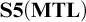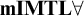FirstView articles
Research Article
WHEN NO PRICE IS RIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRUCTURE OF BOCHVAR ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-27
-
- Article
- Export citation
THE TEMPORAL CONTINUUM
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-19
-
- Article
- Export citation
ARROW’S THEOREM, ULTRAFILTERS, AND REVERSE MATHEMATICS
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONCEPTUAL DISTANCE AND ALGEBRAS OF CONCEPTS
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
AN ALGEBRAIC PROOF OF COMPLETENESS FOR MONADIC FUZZY PREDICATE LOGIC MMTL∀ – ERRATUM
-
- Published online by Cambridge University Press:
- 15 January 2024, p. 1
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
BEYOND LINGUISTIC INTERPRETATION IN THEORY COMPARISON
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-41
-
- Article
- Export citation
PARACONSISTENT AND PARACOMPLETE ZERMELO–FRAENKEL SET THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOGICS FROM ULTRAFILTERS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-FACTIVE KOLMOGOROV CONDITIONALIZATION
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-27
-
- Article
- Export citation
AN ALGEBRAIC PROOF OF COMPLETENESS FOR MONADIC FUZZY PREDICATE LOGIC
 $\mathbf {MMTL}\boldsymbol {\forall }$
$\mathbf {MMTL}\boldsymbol {\forall }$
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2023, pp. 1-27
-
- Article
- Export citation
DECIDABLE FRAGMENTS OF THE QUANTIFIED ARGUMENT CALCULUS
- Part of:
-
- Published online by Cambridge University Press:
- 29 September 2023, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONNEXIVE IMPLICATIONS IN SUBSTRUCTURAL LOGICS
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-32
-
- Article
- Export citation
‘A REMARKABLE ARTIFICE’: LAPLACE, POISSON AND MATHEMATICAL PURITY
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-37
-
- Article
- Export citation
TESTING DEFINITIONAL EQUIVALENCE OF THEORIES VIA AUTOMORPHISM GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1-22
-
- Article
- Export citation
SUBJECT-MATTER AND INTENSIONAL OPERATORS III: STATE-SENSITIVE SUBJECT-MATTER AND TOPIC SUFFICIENCY
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1-27
-
- Article
- Export citation
A NATURAL DEDUCTION SYSTEM FOR ORTHOMODULAR LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SIMPLIFIED PROOF OF THE EPSILON THEOREMS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
-
- Article
- Export citation
RELEVANT CONSEQUENCE RELATIONS: AN INVITATION
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IS CANTOR’S THEOREM A DIALETHEIA? VARIATIONS ON A PARACONSISTENT APPROACH TO CANTOR’S THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1-18
-
- Article
- Export citation