Research Article
Derivations of 2-subhomogeneous C*-algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 449-456
-
- Article
-
- You have access
- Export citation
Limiting behaviours of non-oscillatory solutions of a pair of coupled nonlinear differential equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 457-473
-
- Article
-
- You have access
- Export citation
On the solution sets to differential inclusions on an unbounded interval
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 475-484
-
- Article
-
- You have access
- Export citation
Higher-order estimates for fully nonlinear difference equations. I
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 485-510
-
- Article
-
- You have access
- Export citation
On the essential spectrum of Banach-space operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 511-528
-
- Article
-
- You have access
- Export citation
On the limit cycles of polynomial differential systems with homogeneous nonlinearities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 529-543
-
- Article
-
- You have access
- Export citation
Elliptic problems in ℝN with discontinuous nonlinearities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 545-558
-
- Article
-
- You have access
- Export citation
Rank properties in finite inverse semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 559-568
-
- Article
-
- You have access
- Export citation
Extremal solutions and strong relaxation for nonlinear periodic evolution inclusions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 569-586
-
- Article
-
- You have access
- Export citation
Some examples of critical points for the total mean curvature functional
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 587-603
-
- Article
-
- You have access
- Export citation
Jacobians of singular spectral curves and completely integrable systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 605-623
-
- Article
-
- You have access
- Export citation
On the blow-up and positive entire solutions of semilinear elliptic equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 625-631
-
- Article
-
- You have access
- Export citation
An algorithm for constructing multidimensional biorthogonal periodic multiwavelets
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 633-649
-
- Article
-
- You have access
- Export citation
Infinite metacyclic groups and their non-abelian tensor squares
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 651-662
-
- Article
-
- You have access
- Export citation
Book Reviews
N. J. Hitchin, G. B. Segal and R. S. Ward Integrable systems: twistors, loop groups and Riemann surfaces (Oxford Graduate Texts in Mathematics, vol. 4, Clarendon Press, 1999), ix + 136pp., 0 19 850421 7, £25.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 663-664
-
- Article
-
- You have access
- Export citation
D. M. Bressoud Proofs and confirmations: the story of the alternating sign matrix conjecture (Spectrum Series, Mathematical Association of America/Cambridge University Press, 1999), xv + 274pp., 0 521 66646 5 (paperback), £17.95 (US$29.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 665-666
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 43 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f8
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 43 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

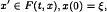
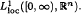
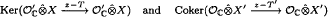
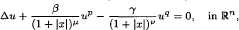
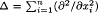 and
and