Research Article
On the complex oscillation for a class of homogeneous linear differential equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
On realization of splitting obstructions in Browder-Livesay groups for closed manifold pairs
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 15-25
-
- Article
-
- You have access
- Export citation
Finitarily linear wreath products
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 27-41
-
- Article
-
- You have access
- Export citation
Triangularizing semigroups of positive operators on an atomic normed Riesz Space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 43-55
-
- Article
-
- You have access
- Export citation
Maximal functions and transference for groups of operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 57-71
-
- Article
-
- You have access
- Export citation
Hilbert-Samuel function and Grothendieck group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 73-94
-
- Article
-
- You have access
- Export citation
Summability of alternating gap series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 95-101
-
- Article
-
- You have access
- Export citation
On the solvability of semilinear differential equations at resonance
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 103-112
-
- Article
-
- You have access
- Export citation
The dynamics of linearized polynomials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 113-128
-
- Article
-
- You have access
- Export citation
On the Weiss conjecture for finite locally primitive graphs
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 129-138
-
- Article
-
- You have access
- Export citation
Linear isometries on subalgebras of uniformly continuous functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-147
-
- Article
-
- You have access
- Export citation
On a question of Milnor concerning singularities of maps
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 149-153
-
- Article
-
- You have access
- Export citation
Discrete focal boundary-value problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 155-165
-
- Article
-
- You have access
- Export citation
The positive cones of k0-groups of crossed products associated with Furstenberg transformations on the 2-torus
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 167-175
-
- Article
-
- You have access
- Export citation
Subgroups of finite index in groups with finite complete rewriting systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 177-183
-
- Article
-
- You have access
- Export citation
Combinatorial L2-determinants
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-194
-
- Article
-
- You have access
- Export citation
Operators having the symmetrized bidisc as a spectral set
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 195-210
-
- Article
-
- You have access
- Export citation
2-groups with few conjugacy classes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 211-217
-
- Article
-
- You have access
- Export citation
Book Reviews
W. Freeden, T. Gervens and M. Schreiner Constructive approximation on the sphere with applications to geomathematics (Numerical Mathematics and Scientific Computation, Clarendon Press, 1998), xv + 427 pp., 0 19 853682 8, £65.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 219-220
-
- Article
-
- You have access
- Export citation
P. C. Roberts Multiplicities and Chern Classes in local algebra (Cambridge Tracts in Mathematics no. 133, Cambridge, 1998), xi + 303 pp., 0 521 47316 0 (hardback), £37.50 (US$59.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 220-221
-
- Article
-
- You have access
- Export citation

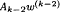 + … +
+ … + 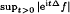 for the Schrödinger group is in
for the Schrödinger group is in 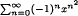 is summable at
is summable at 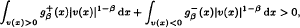
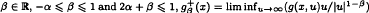 and
and 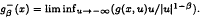
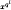 , where
, where 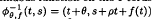 for any (
for any (