Article contents
Summability of alternating gap series
Published online by Cambridge University Press: 20 January 2009
Abstract
The Abel and Cesàro summabilities of two alternating gap series are investigated. We prove that the series 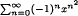 is summable at x = 1 (in both senses), but that
is summable at x = 1 (in both senses), but that 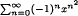 is not. In 1907, Hardy obtained essentially the same result for the latter series; our proof is shorter and more elementary: we use the Poisson summation formula to derive an explicit estimate for the size of the oscillations as x → 1_. This represents an example of a general method for determining the Abel summability of similar series.
is not. In 1907, Hardy obtained essentially the same result for the latter series; our proof is shorter and more elementary: we use the Poisson summation formula to derive an explicit estimate for the size of the oscillations as x → 1_. This represents an example of a general method for determining the Abel summability of similar series.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 1 , February 2000 , pp. 95 - 101
- Copyright
- Copyright © Edinburgh Mathematical Society 2000
References
- 1
- Cited by


