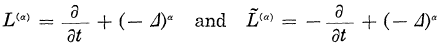Research Article
Algebraic K3 surfaces with finite automorphism groups
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
Homogeneous line bundles over a toroidal group
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 17-24
-
- Article
-
- You have access
- Export citation
Elastic waves in two solids as propagation of singularities phenomenon
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-42
-
- Article
-
- You have access
- Export citation
Infinitely divisible probability measures on a discrete Gelfand pair
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 43-62
-
- Article
-
- You have access
- Export citation
Notes on projective structures on complex manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 63-88
-
- Article
-
- You have access
- Export citation
Kirillov models for distinguished representations
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 89-110
-
- Article
-
- You have access
- Export citation
The family of lines on the Fano threefold V5
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 111-122
-
- Article
-
- You have access
- Export citation
A probabilistic study on the value-distribution of Dirichlet series attached to certain cusp forms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 123-138
-
- Article
-
- You have access
- Export citation
Regular actions of simple algebraic groups on projective threefolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 139-148
-
- Article
-
- You have access
- Export citation
Connection problem in holonomic q-difference system associated with a Jackson integral of Jordan-Pochhammer type
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-161
-
- Article
-
- You have access
- Export citation
The Wiener criterion of regular points for the parabolic operator of order α
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 163-179
-
- Article
-
- You have access
- Export citation
The volumes of small geodesic balls and generalized Chern numbers of Kaehler manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 181-189
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 116 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 116 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



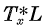 is isomorphic to
is isomorphic to 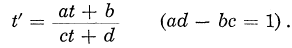
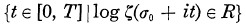
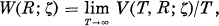
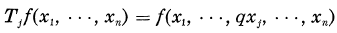
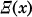 on
on