Research Article
On the class number and unit index of simplest quartic fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-13
-
- Article
-
- You have access
- Export citation
Young diagrammatic methods in non-commutative invariant theory
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 15-34
-
- Article
-
- You have access
- Export citation
Siegel modular forms and theta series attached to quaternion algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 35-96
-
- Article
-
- You have access
- Export citation
The Hecke algebra on the cohomology of Γ0 (p0)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 97-125
-
- Article
-
- You have access
- Export citation
On the Cartan-Norden theorem for affine Kähler immersions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 127-135
-
- Article
-
- You have access
- Export citation
On the topology of full non-degenerate complete intersection variety
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 137-148
-
- Article
-
- You have access
- Export citation
Explicit descriptions of trace rings of generic 2 by 2 matrices
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-159
-
- Article
-
- You have access
- Export citation
A generalization of Hubert’s theorem 94
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 161-169
-
- Article
-
- You have access
- Export citation
On generalized Whittaker functions on Siegel’s upper half space of degree 2
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 171-184
-
- Article
-
- You have access
- Export citation
A Characterization of White Noise Test Functionals
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-194
-
- Article
-
- You have access
- Export citation
On the Strong Unimodality of Lévy Processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 195-199
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 121 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 121 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



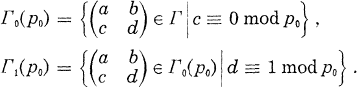
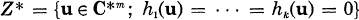
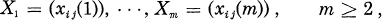
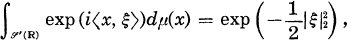
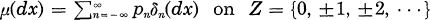 is said to be unimodal with mode
is said to be unimodal with mode