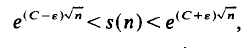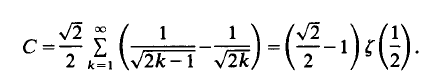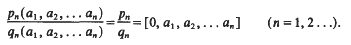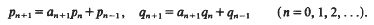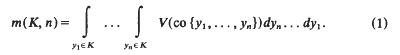Research Article
σ-fragmentable Banach spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-215
-
- Article
- Export citation
Simultaneous additive congruences to a large prime modulus
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
On Bombieri and Davenport's theorem concerning small gaps between primes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-17
-
- Article
- Export citation
Paradoxical decompositions using Lipschitz functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-222
-
- Article
- Export citation
On the Lipschitz equivalence of Cantor sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-233
-
- Article
- Export citation
T-numbers form an M0 set
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-24
-
- Article
- Export citation
An asymptotic formula for a-th powers dividing binomial coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
-
- Article
- Export citation
Regular and ubiquitous systems, and ℳs∞-dense sequences
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 234-243
-
- Article
- Export citation
A problem of Good on Hausdorff dimension
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 244-246
-
- Article
- Export citation
Kac modules of sl (2/2) and the extended Kac-Weyl formulas
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-48
-
- Article
- Export citation
A note on the Krull dimension of certain algebras
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
-
- Article
- Export citation
Estimating sizes of a convex body by successive diameters and widths
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-257
-
- Article
- Export citation
On the Busemann-Petty problem about convex, centrally symmetric bodies in ℝn
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-266
-
- Article
- Export citation
Minimal length functions on groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-61
-
- Article
- Export citation
On some intermediate rings
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-66
-
- Article
- Export citation
Minimal pairs of convex bodies in two dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-273
-
- Article
- Export citation
On the sausage catastrophe in 4-space
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-278
-
- Article
- Export citation
The volume of duals and sections of polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-80
-
- Article
- Export citation
Random polytopes in smooth convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-92
-
- Article
- Export citation
On the mean value of the area of a random polygon in a plane convex body
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-290
-
- Article
- Export citation



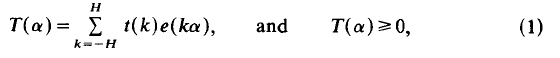
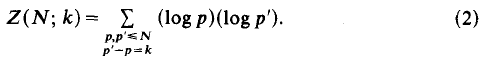
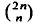 satisfies for arbitrary
satisfies for arbitrary