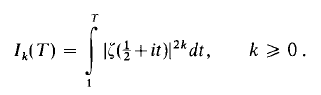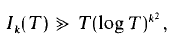Research Article
On certain infinite products II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
-
- Article
- Export citation
An application of Siegel's formula over quaternion orders
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-16
-
- Article
- Export citation
Some relations connecting measures of convergence for series with non-increasing terms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
-
- Article
- Export citation
Rings of fractional dimension
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-27
-
- Article
- Export citation
K-analytic sets: corrigenda et addenda
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 28-32
-
- Article
- Export citation
Sums of distances between points on a sphere — an application of the theory of irregularities of distribution to discrete Geometry
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-41
-
- Article
- Export citation
A very sparse set of dimension 1
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-46
-
- Article
- Export citation
Approximations to the temperature in a heated thermoelastic fluid
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-64
-
- Article
- Export citation
Two-dimensional Stokes flows with cylinders and line singularities
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-75
-
- Article
- Export citation
The Hausdorff distance between compact convex sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-82
-
- Article
- Export citation
A non-Schlegelian polyhedral map on the torus
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-88
-
- Article
- Export citation
The p-periodicity of the groups GL (n, Os(K)) and SL(n, Os(K))
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-97
-
- Article
- Export citation
The average orders of Hooley's Δr-functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-109
-
- Article
- Export citation
On torsion of abelian varieties over large algebraic extensions of finitely generated fields
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 110-116
-
- Article
- Export citation
Sausage-skin problems for finite coverings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-136
-
- Article
- Export citation
A construction of integral lattices
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-140
-
- Article
- Export citation
The divisor function at consecutive integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-149
-
- Article
- Export citation
On some exponential sums connected with Ramanujan's τ-function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 150-158
-
- Article
- Export citation
On mean values of the zeta-function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-161
-
- Article
- Export citation
Front matter
MTK volume 31 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation



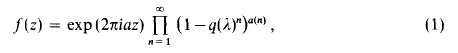

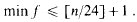
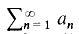 converges; then clearly
converges; then clearly 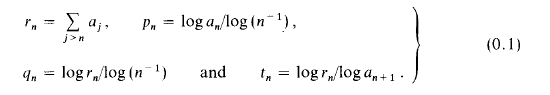
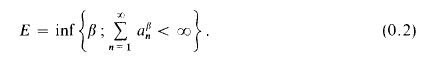
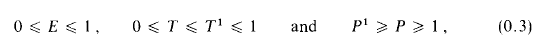
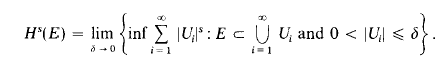
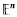 with mean width equal to that of a line segment of length 2 and with Steiner point at the origin is contained in the unit ball. As a consequence, the diameter with respect to the Hausdorff metric of the space of all such sets is 1. There also results a sharp bound for the Hausdorff distance between any two compact convex sets.
with mean width equal to that of a line segment of length 2 and with Steiner point at the origin is contained in the unit ball. As a consequence, the diameter with respect to the Hausdorff metric of the space of all such sets is 1. There also results a sharp bound for the Hausdorff distance between any two compact convex sets.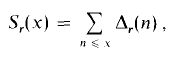
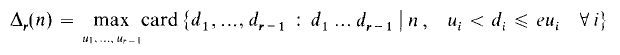
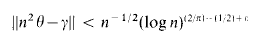
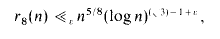
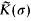 the following results hold.
the following results hold.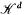 denote the set of convex bodies of
denote the set of convex bodies of 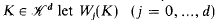 denote the
denote the 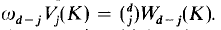 The intrinsic volumes are independent of the dimension of the space in which
The intrinsic volumes are independent of the dimension of the space in which