Research Article
Rotation Invariant Minkowski Classes of Convex Bodies
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 1-13
-
- Article
- Export citation
Nakajima's Problem: Convex Bodies of Constant Width and Constant Brightness
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 15-24
-
- Article
- Export citation
The Upper-Bound Theorem for Families of Boxes in ℝd
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 25-34
-
- Article
- Export citation
Variations of Classic Characterizations of Ellipsoids and a Short Proof of the False Centre Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 35-40
-
- Article
- Export citation
Shaken False Centre Theorem, I
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 41-46
-
- Article
- Export citation
Weights of Modular Forms on so+(2, l) and Congruences Between Eisenstein Series and Cusp forms of Half-Integral Weight on SL2
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 47-58
-
- Article
- Export citation
On Construction of Saturated Distinguished Chains
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 59-65
-
- Article
- Export citation
Products of Weak P-Spaces and K-Analytic Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 67-81
-
- Article
- Export citation
On Integer Polynomials with Multiple Roots
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 83-92
-
- Article
- Export citation
Counting Rational Points on Cubic Hypersurfaces
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 93-112
-
- Article
- Export citation
A Discrete Mean Value of the Derivative of the Riemann Zeta Function
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 113-155
-
- Article
- Export citation
A note on the motion of an Ocean Bacterium in a Linear Shear Flow
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 157-160
-
- Article
- Export citation
Numerically Optimized Markovian Coupling and Mixing in One-Dimensional Maps
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 161-181
-
- Article
- Export citation
On the Asymptotic Expansion of a Class of Functions Defined by Infinite Integrals
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 183-195
-
- Article
- Export citation



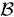 be a family of axis-aligned parallelotopes, or boxes, in ℝ
be a family of axis-aligned parallelotopes, or boxes, in ℝ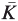 of
of