Research Article
Decomposable convex polyhedra
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-95
-
- Article
- Export citation
Algebraic integral representations by arbitrary forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-100
-
- Article
- Export citation
A problem of Dade on quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-106
-
- Article
- Export citation
A note on cracks under longitudinal shear
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-113
-
- Article
- Export citation
An elementary derivation of certain homological inequalities
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 114-124
-
- Article
- Export citation
Rational polygons
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
-
- Article
- Export citation
Coprime mappings between sets of consecutive integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-136
-
- Article
- Export citation
Sums of m-th powers in p-adic rings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-146
-
- Article
- Export citation
A Stokes flow problem between two non-concentric cylinders
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-156
-
- Article
- Export citation
Covering a sphere with spheres
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-164
-
- Article
- Export citation
Indexes
Index to volume 10
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 165
-
- Article
- Export citation
Index to Volume 1–10 1954–1963
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-182
-
- Article
- Export citation
Front matter
MTK volume 10 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation




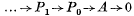
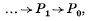
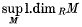 is called the
is called the 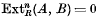 for all left
for all left 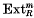 regarded as a functor of left
regarded as a functor of left