Article contents
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
Published online by Cambridge University Press: 28 January 2016
Abstract
We study the meromorphic continuation and the spectral expansion of the opposite-sign Kloosterman sum zeta function 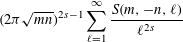 $$\begin{eqnarray}\displaystyle (2{\it\pi}\sqrt{mn})^{2s-1}\mathop{\sum }_{\ell =1}^{\infty }\frac{S(m,-n,\ell )}{\ell ^{2s}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (2{\it\pi}\sqrt{mn})^{2s-1}\mathop{\sum }_{\ell =1}^{\infty }\frac{S(m,-n,\ell )}{\ell ^{2s}} & & \displaystyle \nonumber\end{eqnarray}$$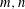 $m,n$ positive integers, to all
$m,n$ positive integers, to all 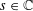 $s\in \mathbb{C}$. There are poles of the function corresponding to zeros of the Riemann zeta function and the spectral parameters of Maass forms. The analytic properties of this function are rather delicate. It turns out that the spectral expansion of the zeta function converges only in a left half-plane, disjoint from the region of absolute convergence of the Dirichlet series, even though they both are analytic expressions of the same meromorphic function on the entire complex plane.
$s\in \mathbb{C}$. There are poles of the function corresponding to zeros of the Riemann zeta function and the spectral parameters of Maass forms. The analytic properties of this function are rather delicate. It turns out that the spectral expansion of the zeta function converges only in a left half-plane, disjoint from the region of absolute convergence of the Dirichlet series, even though they both are analytic expressions of the same meromorphic function on the entire complex plane.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 2
- Cited by




