Article contents
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS
Published online by Cambridge University Press: 22 January 2016
Abstract
Let 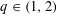 $q\in (1,2)$. A
$q\in (1,2)$. A 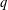 $q$-expansion of a number
$q$-expansion of a number  $x$ in
$x$ in 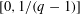 $[0,1/(q-1)]$ is a sequence
$[0,1/(q-1)]$ is a sequence 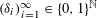 $({\it\delta}_{i})_{i=1}^{\infty }\in \{0,1\}^{\mathbb{N}}$ satisfying
$({\it\delta}_{i})_{i=1}^{\infty }\in \{0,1\}^{\mathbb{N}}$ satisfying 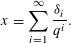 $$\begin{eqnarray}x=\mathop{\sum }_{i=1}^{\infty }\frac{{\it\delta}_{i}}{q^{i}}.\end{eqnarray}$$
$$\begin{eqnarray}x=\mathop{\sum }_{i=1}^{\infty }\frac{{\it\delta}_{i}}{q^{i}}.\end{eqnarray}$$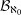 ${\mathcal{B}}_{\aleph _{0}}$ denote the set of
${\mathcal{B}}_{\aleph _{0}}$ denote the set of 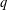 $q$ for which there exists
$q$ for which there exists  $x$ with a countable number of
$x$ with a countable number of 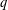 $q$-expansions, and let
$q$-expansions, and let 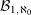 ${\mathcal{B}}_{1,\aleph _{0}}$ denote the set of
${\mathcal{B}}_{1,\aleph _{0}}$ denote the set of 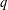 $q$ for which
$q$ for which 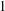 $1$ has a countable number of
$1$ has a countable number of 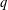 $q$-expansions. In Erdős et al [On the uniqueness of the expansions
$q$-expansions. In Erdős et al [On the uniqueness of the expansions 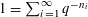 $1=\sum _{i=1}^{\infty }q^{-n_{i}}$. Acta Math. Hungar.58 (1991), 333–342] it was shown that
$1=\sum _{i=1}^{\infty }q^{-n_{i}}$. Acta Math. Hungar.58 (1991), 333–342] it was shown that 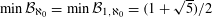 $\min {\mathcal{B}}_{\aleph _{0}}=\min {\mathcal{B}}_{1,\aleph _{0}}=(1+\sqrt{5})/2$, and in S. Baker [On small bases which admit countably many expansions. J. Number Theory147 (2015), 515–532] it was shown that
$\min {\mathcal{B}}_{\aleph _{0}}=\min {\mathcal{B}}_{1,\aleph _{0}}=(1+\sqrt{5})/2$, and in S. Baker [On small bases which admit countably many expansions. J. Number Theory147 (2015), 515–532] it was shown that 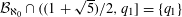 ${\mathcal{B}}_{\aleph _{0}}\cap ((1+\sqrt{5})/2,q_{1}]=\{q_{1}\}$, where
${\mathcal{B}}_{\aleph _{0}}\cap ((1+\sqrt{5})/2,q_{1}]=\{q_{1}\}$, where 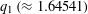 $q_{1}\,({\approx}1.64541)$ is the positive root of
$q_{1}\,({\approx}1.64541)$ is the positive root of 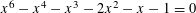 $x^{6}-x^{4}-x^{3}-2x^{2}-x-1=0$. In this paper we show that the second smallest point of
$x^{6}-x^{4}-x^{3}-2x^{2}-x-1=0$. In this paper we show that the second smallest point of 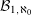 ${\mathcal{B}}_{1,\aleph _{0}}$ is
${\mathcal{B}}_{1,\aleph _{0}}$ is 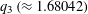 $q_{3}\,({\approx}1.68042)$, the positive root of
$q_{3}\,({\approx}1.68042)$, the positive root of 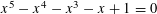 $x^{5}-x^{4}-x^{3}-x+1=0$. En route to proving this result, we show that
$x^{5}-x^{4}-x^{3}-x+1=0$. En route to proving this result, we show that 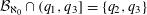 ${\mathcal{B}}_{\aleph _{0}}\cap (q_{1},q_{3}]=\{q_{2},q_{3}\}$, where
${\mathcal{B}}_{\aleph _{0}}\cap (q_{1},q_{3}]=\{q_{2},q_{3}\}$, where 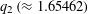 $q_{2}\,({\approx}1.65462)$ is the positive root of
$q_{2}\,({\approx}1.65462)$ is the positive root of 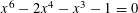 $x^{6}-2x^{4}-x^{3}-1=0$.
$x^{6}-2x^{4}-x^{3}-1=0$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 3
- Cited by




