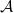FirstView articles
Special Issue: LSFA 2021 and LSFA 2022
A linear linear lambda-calculus
-
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-35
-
- Article
- Export citation
Paper
Countability constraints in order-theoretic approaches to computability
-
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special Issue: Logic, Databases and Complexity
Logical characterizations of algebraic circuit classes over integral domains
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special Issue: Advances in Homotopy type theory
On planarity of graphs in homotopy type theory
-
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special Issue: WoLLIC 2022
Abstract cyclic proofs
-
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
You can only be lucky once: optimal gossip for epistemic goals
-
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special Issue: LSFA 2021 and LSFA 2022
Equational theorem proving for clauses over strings
-
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Paper
New and improved bounds on the contextuality degree of multi-qubit configurations
-
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-22
-
- Article
- Export citation
A 2-categorical proof of Frobenius for fibrations defined from a generic point
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special Issue: Logic, Databases and Complexity
Dimension in team semantics
-
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-45
-
- Article
- Export citation
Special Issue: WoLLIC 2022
Implicational Kleene algebra with domain and the substructural logic of partial correctness
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-16
-
- Article
- Export citation
Special Issue: Logic, Databases and Complexity
Parameterized complexity of weighted team definability
-
- Published online by Cambridge University Press:
- 20 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Game characterizations for the number of quantifiers
-
- Published online by Cambridge University Press:
- 10 January 2024, pp. 1-20
-
- Article
- Export citation
Special Issue: WoLLIC 2022
Visibility and exploitation in social networks
-
- Published online by Cambridge University Press:
- 19 December 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Material dialogues for first-order logic in constructive type theory: extended version
-
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation