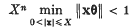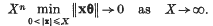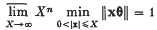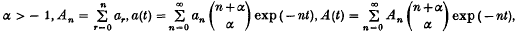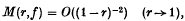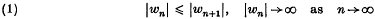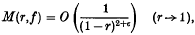Research Article
A compact space having the cardinality of the continuum with no convergent sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-181
-
- Article
- Export citation
Nets of conics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-364
-
- Article
- Export citation
Large cycles in large labelled graphs. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-2
-
- Article
- Export citation
Zero divisors and idempotents in group rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-368
-
- Article
- Export citation
Jordan algebras spanned by Hermitian elements of a Banach algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 3-13
-
- Article
- Export citation
A simple proof of an identity of Good
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-184
-
- Article
- Export citation
On the growth of recurrence sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-376
-
- Article
- Export citation
Canonical extensions for embeddings of topological spheres of any codimension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-24
-
- Article
- Export citation
The maximal subgroups of M24
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 185-192
-
- Article
- Export citation
Vector lattices freely generated by distributive lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-200
-
- Article
- Export citation
Completeness and intertwined completeness of locally convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-30
-
- Article
- Export citation
Singular n-tuples and Hausdorff dimension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-385
-
- Article
- Export citation
Irreducible representations of finitely generated nilpotent groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-208
-
- Article
- Export citation
Perturbations by operators converging compactly to zero
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-391
-
- Article
- Export citation
Riesz spaces with the order-continuity property. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-42
-
- Article
- Export citation
The remainder in a gap Tauberian theorem for Abel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-45
-
- Article
- Export citation
On finite groups containing no element of order six
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-224
-
- Article
- Export citation
The homology of BO and some results about the Steenrod algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-398
-
- Article
- Export citation
Weakly prime compact convex sets and uniform algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 225-232
-
- Article
- Export citation
Means and coefficients of functions which omit a sequence of values
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 47-57
-
- Article
- Export citation