Research Article
On generalized albanese varieties for surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-6
-
- Article
- Export citation
Stably continuous frames
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 7-19
-
- Article
- Export citation
Pregroups and length functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 21-30
-
- Article
- Export citation
Filtrations, closure operations and prime divisors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-46
-
- Article
- Export citation
Locally compact groups: maximal compact subgroups and N-groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 47-64
-
- Article
- Export citation
Rational homotopy equivalences of Lie type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 65-80
-
- Article
- Export citation
Group homomorphisms inducing an isomorphism of a functor: Dedicated to Professor Nobuo Shimada on his 60th birthday
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-93
-
- Article
- Export citation
The loops on U(n)/O(n) and U(2n)/Sp(n)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-103
-
- Article
- Export citation
An evaluation of the Jones polynomial of a parallel link
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 105-113
-
- Article
- Export citation
Tangential H∞-images of boundary curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-118
-
- Article
- Export citation
Geometry of the tensor product of C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-127
-
- Article
- Export citation
Dirichlet forms on partial *-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-140
-
- Article
- Export citation
Statistical convergence in a locally convex space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 141-145
-
- Article
- Export citation
Random dissections and branching processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-151
-
- Article
- Export citation
The Stokes constants for a cluster of transition points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-179
-
- Article
- Export citation
Symmetry relations for connection matrices in the phase-integral method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 181-191
-
- Article
- Export citation
Front matter
PSP volume 104 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 104 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation



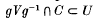 for each
for each 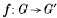
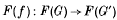 (
(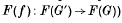 ,
, 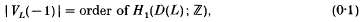
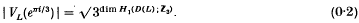


 and ℬ are C*-algebras their algebraic tensor product
and ℬ are C*-algebras their algebraic tensor product