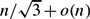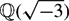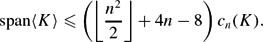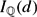Research Article
Slow increasing functions and the largest partial quotients in continued fraction expansions
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 1-14
-
- Article
- Export citation
The Delaunay tessellation in hyperbolic space
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 15-46
-
- Article
- Export citation
Expected number of real zeros for random orthogonal polynomials
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 47-66
-
- Article
- Export citation
On the p-part of the Birch–Swinnerton-Dyer conjecture for elliptic curves with complex multiplication by the ring of integers of
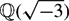 $\mathbbQ(\sqrt-3)$
$\mathbbQ(\sqrt-3)$
-
- Published online by Cambridge University Press:
- 17 October 2016, pp. 67-98
-
- Article
- Export citation
Effective irrationality measures for real and p-adic roots of rational numbers close to 1, with an application to parametric families of Thue–Mahler equations
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 99-108
-
- Article
- Export citation
Surgery on tori in the 4–sphere
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 109-124
-
- Article
- Export citation
Directed complete poset models of T1 spaces
-
- Published online by Cambridge University Press:
- 11 October 2016, pp. 125-134
-
- Article
- Export citation
Open projections and suprema in the Cuntz semigroup
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 135-146
-
- Article
- Export citation
Multi-crossing number for knots and the Kauffman bracket polynomial
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 147-178
-
- Article
- Export citation
Isogenies of non-CM elliptic curves with rational j-invariants over number fields
-
- Published online by Cambridge University Press:
- 01 March 2017, pp. 179-184
-
- Article
- Export citation
A note on the topological sliceness of some 2-bridge knots
-
- Published online by Cambridge University Press:
- 17 March 2017, pp. 185-191
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 164 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 December 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 164 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 December 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation