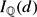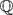Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Le Fourn, Samuel
and
Lemos, Pedro
2021.
Residual Galois representations of elliptic curves with image contained in the normaliser of a nonsplit Cartan.
Algebra & Number Theory,
Vol. 15,
Issue. 3,
p.
747.
Cremona, J. E.
and
Najman, Filip
2021.
$${{\mathbb {Q}}}$$-curves over odd degree number fields.
Research in Number Theory,
Vol. 7,
Issue. 4,
Banwait, Barinder
Najman, Filip
and
Padurariu, Oana
2023.
Cyclic isogenies of elliptic curves over fixed quadratic fields.
Mathematics of Computation,
Vol. 93,
Issue. 346,
p.
841.
Najman, Filip
and
Vukorepa, Borna
2023.
Quadratic points on bielliptic modular curves.
Mathematics of Computation,
Vol. 92,
Issue. 342,
p.
1791.