Hostname: page-component-7bb8b95d7b-wpx69 Total loading time: 0 Render date: 2024-09-07T12:49:06.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Double Meijer transformations of certain hypergeometric functions

Published online by Cambridge University Press:  24 October 2008

H. M. Srivastava  and
J. P. Singhal
H. M. Srivastava
Affiliation:
Department of Mathematics, The University, Jodhpur, India
J. P. Singhal
Affiliation:
Department of Mathematics, The University, Jodhpur, India
Get access Rights & Permissions [Opens in a new window]

Extract

Following the usual notation for generalized hypergeometric functions we let

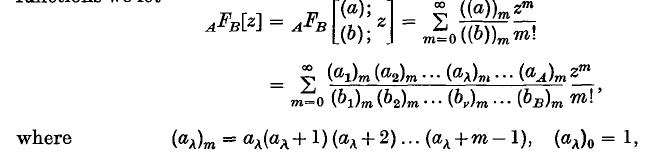
(a) denotes the sequence of A parameters

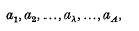
that is, there are A of the a parameters and B of the b parameters. Thus ((a))m has the interpretation

with a similar interpretation for ((b))m; Δ(k; α) stands for the set of k parameters

and for the sake of brevity, the pair of parameters like α + β, α − β will be written as α ± β, the gamma product Γ(α + β) Γ(α − β) as Γ(α ± β), and so on.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 2 , April 1968 , pp. 425 - 430
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Abdul-Halim, N. and Al-Salam, W. A.Double Euler transformations of certain hypergeometric functions. Duke Math. J. 30 (1963), 51–62.CrossRefGoogle Scholar
(2)Al-Salam, W. A.The Bessel polynomials. Duke Math. J. 24 (1957), 529–547.CrossRefGoogle Scholar
(3)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, vol. I (McGraw-Hill; New York, 1953).Google Scholar
(4)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, vol. II (McGraw-Hill; New York, 1953).Google Scholar
(5)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, vol. II (McGraw-Hill; New York, 1955).Google Scholar
(6)Krall, H. L. and Frink, O.A new class of orthogonal polynomials: the Bessel polynomials. Trans. Amer. Math. Soc. 65 (1949), 100–115.CrossRefGoogle Scholar
(7)Rainville, E. D.Special functions (Macmillan; New York, 1960).Google Scholar
(8)Singh, R. P.A note on double transformations of certain hypergeometric functions. Proc. Edinburgh Math. Soc. (2), 14 (1965), 221–227.CrossRefGoogle Scholar
(9)Slater, L. J.Confluent hypergeometric functions (Cambridge, 1960).Google Scholar
(10)Slater, L. J.Generalized hypergeometric functions (Cambridge, 1966).Google Scholar
(11)Srivastava, H. M.On Bessel, Jacobi and Laguerre polynomials. Rend. Sem. Mat. Univ. Padova. 35 (1965), 424–432.Google Scholar
(12)Srivastava, H. M.Some expansions in products of hypergeometric functions. Proc. Cambridge Philos. Soc. 62 (1966), 245–247.CrossRefGoogle Scholar
(13)Srivastava, H. M.The integration of generalized hypergeometric functions. Proc. Cambridge Philos. Soc. 62 (1966), 761–764.CrossRefGoogle Scholar
(14)Srivastava, H. M.The products of certain classical polynomials. Math. Japon. 11 (1966), 67–76.Google Scholar
(15)Watson, G. N.Theory of Bessel functions (Cambridge, 1944).Google Scholar