Research Article
A problem of bounded expressibility in free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 573-584
-
- Article
- Export citation
On a construction due to P. M. Cohn
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-250
-
- Article
- Export citation
Note on a problem of Porte
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 1
-
- Article
- Export citation
On ideals of finite homoloǵical dimension in local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 941-948
-
- Article
- Export citation
Kruskal's theorem for matroids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 3-4
-
- Article
- Export citation
Bezout rings and their subrings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-264
-
- Article
- Export citation
A note on the homology of ideals ǵenerated by three elements in local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 949-952
-
- Article
- Export citation
A characterization of sets of n points which determine n hyperplanes†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 585-588
-
- Article
- Export citation
Subplanes of the Hughes plane of order 9
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 589-598
-
- Article
- Export citation
A generalization of the chromatic number†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-271
-
- Article
- Export citation
An automorphism of the symplectic group Sp4(2n)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-9
-
- Article
- Export citation
On the complexes of Hirsch and Eilenberǵ–Moore
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 953-960
-
- Article
- Export citation
On better-quasi-ordering transfinite sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-290
-
- Article
- Export citation
A group with zero homology
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 599-602
-
- Article
- Export citation
Products in homotopy groups with certain prime coefficients
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-14
-
- Article
- Export citation
A proof of Newman's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 961-963
-
- Article
- Export citation
Separation axioms for topological ordered spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 965-973
-
- Article
- Export citation
Plane separation
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 291
-
- Article
- Export citation
Cohomology operations and duality
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-30
-
- Article
- Export citation
An algorithm for the construction of 3-manifolds from 2-complexes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 603-614
-
- Article
- Export citation

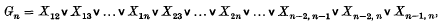
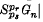 is provable whenever
is provable whenever 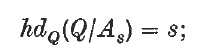
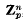 , unique up to homotopy type, such that
, unique up to homotopy type, such that
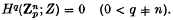
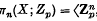 , the group of pointed homotopy classes of pointed maps from
, the group of pointed homotopy classes of pointed maps from 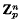 to
to 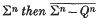
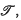 , <) is a set
, <) is a set 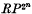 cannot be embedded in
cannot be embedded in 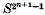 can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories
can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories 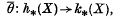
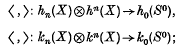
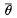 can be turned into a cohomology operation
can be turned into a cohomology operation