Cohomology operations and duality
Published online by Cambridge University Press: 24 October 2008
Extract
Since Thom first introduced the notion of the ‘dual’ of a Steenrod square, in (12), it has become apparent that calculation with such duals in the cohomology of, say, a simplicial complex X will often yield information about the impossibility of embedding X in Sn, for certain values of n. For example, the celebrated theorem that 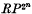 cannot be embedded in
cannot be embedded in 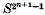 can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories h* and k*, and natural stable cohomology operation θ: h* → k*. We show in section 3 that a simplicial embeddingf: X → Sn gives rise via the Alexander duality isomorphism to a homology operation
can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories h* and k*, and natural stable cohomology operation θ: h* → k*. We show in section 3 that a simplicial embeddingf: X → Sn gives rise via the Alexander duality isomorphism to a homology operation
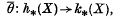
which is independent of n, the particular embedding f, and even the particular triangulations of X and Sn. If h* and k* are multiplicative cohomology theories, there are Kronecker products
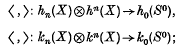
if h0(S0) = k0(S0) = G, a field, and the Kronecker products make h*, h* and k*, k* into dual vector spaces over G, then 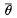 can be turned into a cohomology operation c(θ): k*(X)→h*(X), by using this duality. This is certainly true if h* = k* = H*(;Zp), p prime, and in this case we have the original situation considered by Thom, who showed, for example, that
can be turned into a cohomology operation c(θ): k*(X)→h*(X), by using this duality. This is certainly true if h* = k* = H*(;Zp), p prime, and in this case we have the original situation considered by Thom, who showed, for example, that
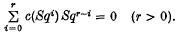
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 1 , January 1968 , pp. 15 - 30
- Copyright
- Copyright © Cambridge Philosophical Society 1968
References
REFERENCES
- 1
- Cited by




