Research Article
On a construction due to P. M. Cohn
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-250
-
- Article
- Export citation
Bezout rings and their subrings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-264
-
- Article
- Export citation
A generalization of the chromatic number†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-271
-
- Article
- Export citation
On better-quasi-ordering transfinite sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-290
-
- Article
- Export citation
Plane separation
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 291
-
- Article
- Export citation
Démonstration du théorème sur la suite spectrale des fibrés au sens de Kan
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-297
-
- Article
- Export citation
The fundamental group of the orbit space of a discontinuous group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-301
-
- Article
- Export citation
Nilpotent groups and compact 3-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 303-306
-
- Article
- Export citation
On differentiable manifolds with degenerate metrics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-316
-
- Article
- Export citation
A quotient ordered space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-322
-
- Article
- Export citation
Uniform approximation by Fourier–Stieltjes transforms†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 323-333
-
- Article
- Export citation
Paranormed sequence spaces generated by infinite matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-340
-
- Article
- Export citation
Sequential convergence in locally convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-364
-
- Article
- Export citation
Stability of wedges and semi-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-376
-
- Article
- Export citation
Absolute summability of infinite series on a scale of Abel type summability methods
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-387
-
- Article
- Export citation
A note on Riesz means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-392
-
- Article
- Export citation
Sums associated with Farey series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-398
-
- Article
- Export citation
On a generalized L–H transform
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-406
-
- Article
- Export citation
On a generalized Stieltjes transform
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-412
-
- Article
- Export citation
A new expansion formula for hypergeometric functions of two variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-416
-
- Article
- Export citation



 ), an equivalence relation
), an equivalence relation 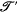 may be defined for the set
may be defined for the set 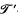 -open if and only if
-open if and only if 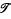 -open in
-open in 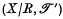 is known as the
is known as the 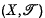 ) and projection
) and projection 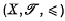 (or simply
(or simply 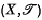 ) since the symbol ≤ denotes all partial orders and no confusion arises) is a topological ordered space (that is,
) since the symbol ≤ denotes all partial orders and no confusion arises) is a topological ordered space (that is, 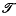 and a partial order ≤ is defined) then, providing the projection
and a partial order ≤ is defined) then, providing the projection 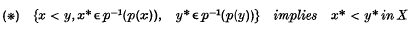
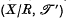 is known as the
is known as the 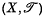 and projection
and projection 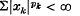 and
and 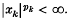 Throughout, sums and suprema without limits are taken from 1 to ∞. Simons (3) considered only the case in which 0 <
Throughout, sums and suprema without limits are taken from 1 to ∞. Simons (3) considered only the case in which 0 < 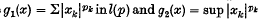 in
in