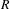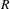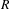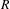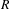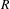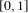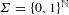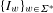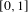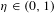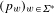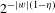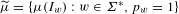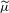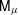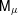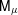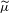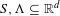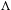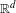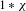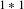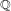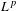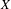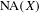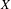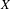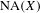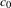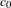Let  $\unicode[STIX]{x1D707}$ be the projection on
$\unicode[STIX]{x1D707}$ be the projection on 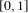 $[0,1]$ of a Gibbs measure on
$[0,1]$ of a Gibbs measure on 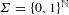 $\unicode[STIX]{x1D6F4}=\{0,1\}^{\mathbb{N}}$ (or more generally a Gibbs capacity) associated with a Hölder potential. The thermodynamic and multifractal properties of
$\unicode[STIX]{x1D6F4}=\{0,1\}^{\mathbb{N}}$ (or more generally a Gibbs capacity) associated with a Hölder potential. The thermodynamic and multifractal properties of  $\unicode[STIX]{x1D707}$ are well known to be linked via the multifractal formalism. We study the impact of a random sampling procedure on this structure. More precisely, let
$\unicode[STIX]{x1D707}$ are well known to be linked via the multifractal formalism. We study the impact of a random sampling procedure on this structure. More precisely, let 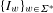 $\{{I_{w}\}}_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ stand for the collection of dyadic subintervals of
$\{{I_{w}\}}_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ stand for the collection of dyadic subintervals of 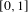 $[0,1]$ naturally indexed by the finite dyadic words. Fix
$[0,1]$ naturally indexed by the finite dyadic words. Fix 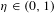 $\unicode[STIX]{x1D702}\in (0,1)$, and a sequence
$\unicode[STIX]{x1D702}\in (0,1)$, and a sequence 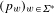 $(p_{w})_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ of independent Bernoulli variables of parameters
$(p_{w})_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ of independent Bernoulli variables of parameters 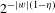 $2^{-|w|(1-\unicode[STIX]{x1D702})}$. We consider the (very sparse) remaining values
$2^{-|w|(1-\unicode[STIX]{x1D702})}$. We consider the (very sparse) remaining values 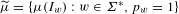 $\widetilde{\unicode[STIX]{x1D707}}=\{\unicode[STIX]{x1D707}(I_{w}):w\in \unicode[STIX]{x1D6F4}^{\ast },p_{w}=1\}$. We study the geometric and statistical information associated with
$\widetilde{\unicode[STIX]{x1D707}}=\{\unicode[STIX]{x1D707}(I_{w}):w\in \unicode[STIX]{x1D6F4}^{\ast },p_{w}=1\}$. We study the geometric and statistical information associated with  $\widetilde{\unicode[STIX]{x1D707}}$, and the relation between
$\widetilde{\unicode[STIX]{x1D707}}$, and the relation between 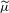 $\widetilde{\unicode[STIX]{x1D707}}$ and
$\widetilde{\unicode[STIX]{x1D707}}$ and  $\unicode[STIX]{x1D707}$. To do so, we construct a random capacity
$\unicode[STIX]{x1D707}$. To do so, we construct a random capacity 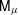 $\mathsf{M}_{\unicode[STIX]{x1D707}}$ from
$\mathsf{M}_{\unicode[STIX]{x1D707}}$ from  $\widetilde{\unicode[STIX]{x1D707}}$. This new object fulfills the multifractal formalism, and its free energy is closely related to that of
$\widetilde{\unicode[STIX]{x1D707}}$. This new object fulfills the multifractal formalism, and its free energy is closely related to that of  $\unicode[STIX]{x1D707}$. Moreover, the free energy of
$\unicode[STIX]{x1D707}$. Moreover, the free energy of 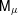 $\mathsf{M}_{\unicode[STIX]{x1D707}}$ generically exhibits one first order and one second order phase transition, while that of
$\mathsf{M}_{\unicode[STIX]{x1D707}}$ generically exhibits one first order and one second order phase transition, while that of  $\unicode[STIX]{x1D707}$ is analytic. The geometry of
$\unicode[STIX]{x1D707}$ is analytic. The geometry of 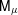 $\mathsf{M}_{\unicode[STIX]{x1D707}}$ is deeply related to the combination of approximation by dyadic numbers with geometric properties of Gibbs measures. The possibility to reconstruct
$\mathsf{M}_{\unicode[STIX]{x1D707}}$ is deeply related to the combination of approximation by dyadic numbers with geometric properties of Gibbs measures. The possibility to reconstruct  $\unicode[STIX]{x1D707}$ from
$\unicode[STIX]{x1D707}$ from 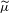 $\widetilde{\unicode[STIX]{x1D707}}$ by using the almost multiplicativity of
$\widetilde{\unicode[STIX]{x1D707}}$ by using the almost multiplicativity of  $\unicode[STIX]{x1D707}$ and concatenation of words is discussed as well.
$\unicode[STIX]{x1D707}$ and concatenation of words is discussed as well.
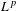 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN