Article contents
EQUIVALENT NORMS WITH AN EXTREMELY NONLINEABLE SET OF NORM ATTAINING FUNCTIONALS
Published online by Cambridge University Press: 13 February 2018
Abstract
We present a construction that enables one to find Banach spaces 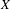 $X$ whose sets
$X$ whose sets 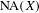 $\operatorname{NA}(X)$ of norm attaining functionals do not contain two-dimensional subspaces and such that, consequently,
$\operatorname{NA}(X)$ of norm attaining functionals do not contain two-dimensional subspaces and such that, consequently, 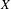 $X$ does not contain proximinal subspaces of finite codimension greater than one, extending the results recently provided by Read [Banach spaces with no proximinal subspaces of codimension 2, Israel J. Math. (to appear)] and Rmoutil [Norm-attaining functionals need not contain 2-dimensional subspaces, J. Funct. Anal. 272 (2017), 918–928]. Roughly speaking, we construct an equivalent renorming with the requested properties for every Banach space
$X$ does not contain proximinal subspaces of finite codimension greater than one, extending the results recently provided by Read [Banach spaces with no proximinal subspaces of codimension 2, Israel J. Math. (to appear)] and Rmoutil [Norm-attaining functionals need not contain 2-dimensional subspaces, J. Funct. Anal. 272 (2017), 918–928]. Roughly speaking, we construct an equivalent renorming with the requested properties for every Banach space 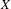 $X$ where the set
$X$ where the set 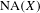 $\operatorname{NA}(X)$ for the original norm is not “too large”. The construction can be applied to every Banach space containing
$\operatorname{NA}(X)$ for the original norm is not “too large”. The construction can be applied to every Banach space containing 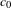 $c_{0}$ and having a countable system of norming functionals, in particular, to separable Banach spaces containing
$c_{0}$ and having a countable system of norming functionals, in particular, to separable Banach spaces containing 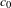 $c_{0}$. We also provide some geometric properties of the norms we have constructed.
$c_{0}$. We also provide some geometric properties of the norms we have constructed.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 259 - 279
- Copyright
- © Cambridge University Press 2018
References
- 5
- Cited by


