Research Article
Formal languages defined by the underlying structure of their words
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1009-1026
-
- Article
- Export citation
Some properties of large filters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1027-1035
-
- Article
- Export citation
Constructive validity is nonarithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1036-1041
-
- Article
- Export citation
Markov's principle, isols and Dedekind finite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1042-1069
-
- Article
- Export citation
Definability and initial segments of c-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1070-1081
-
- Article
- Export citation
On parameter free induction schemas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1082-1097
-
- Article
- Export citation
On the use of inaccessible numbers and order indiscernibles in lower bound arguments for random access machines
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1098-1109
-
- Article
- Export citation
Degree theoretical splitting properties of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1110-1137
-
- Article
- Export citation
On the structure of semialgebraic sets over p-adic fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1138-1164
-
- Article
- Export citation
Sheaves of continuous definable functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1165-1169
-
- Article
- Export citation
On universal semiregular invariant measures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1170-1176
-
- Article
- Export citation
On the validity of hilbert's nullstellensatz, artin's theorem, and related results in grothendieck toposes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1177-1187
-
- Article
- Export citation
Souslin forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1188-1207
-
- Article
- Export citation
Ultrapowers without the axiom of choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1208-1219
-
- Article
- Export citation
The false assumption underlying berry's paradox1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1220-1223
-
- Article
- Export citation
A basis result in combinatory logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1224-1226
-
- Article
- Export citation
Indécidabilité de corps de séries formelles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1227-1234
-
- Article
- Export citation
Provability of the pigeonhole principle and the existence of infinitely many primes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1235-1244
-
- Article
- Export citation
Mechanical learners pay a price for Bayesianism
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1245-1251
-
- Article
- Export citation
Reviews
Alberto Coffa. Carnap, Tarski and the search for truth. Noûs, vol. 21 (1987), pp. 547–572.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1252-1253
-
- Article
- Export citation

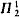 singleton. Groszek built an initial segment of order type 1 +
singleton. Groszek built an initial segment of order type 1 + 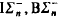 (induction and collection schemas for parameter free
(induction and collection schemas for parameter free 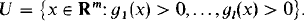
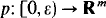
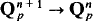 . Analytic maps are maps whose coordinate functions are given locally by convergent power series.
. Analytic maps are maps whose coordinate functions are given locally by convergent power series.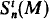 be the space of complete
be the space of complete 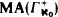 , and using the results on Souslin forcing we show that
, and using the results on Souslin forcing we show that 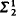 -measurability.
-measurability.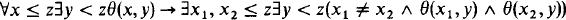
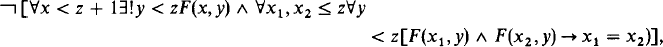
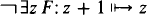 .
.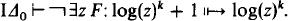
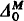 be those subsets of
be those subsets of 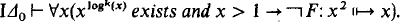
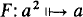 with
with 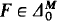 and
and