No CrossRef data available.
Article contents
Definability and initial segments of c-degrees
Published online by Cambridge University Press: 12 March 2014
Abstract
We combine two techniques of set theory relating to mininal degrees of constructibility. Jensen constructed a minimal real which is additionally a 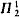 singleton. Groszek built an initial segment of order type 1 + α*, for any ordinal α. This paper shows how to force a
singleton. Groszek built an initial segment of order type 1 + α*, for any ordinal α. This paper shows how to force a 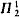 singleton such that the c-degrees beneath it, all represented by reals, are of type 1 + α*, for many ordinals α. We also examine the definability α needs to be so represented by a real.
singleton such that the c-degrees beneath it, all represented by reals, are of type 1 + α*, for many ordinals α. We also examine the definability α needs to be so represented by a real.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988




