Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T18:46:20.171Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on valuation definable expansions of fields

Published online by Cambridge University Press:  12 March 2014

Deirdre Haskell  and
Dugald Macpherson
Deirdre Haskell
Affiliation:
Mathematics Department, College of the Holy Cross, Worcester MA 01610, USA, E-mail: haskell@math.holycross.edu
Dugald Macpherson
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, England, E-mail: pmthdm@amsta.leeds.ac.uk
Get access Rights & Permissions [Opens in a new window]

Extract

In this note, we consider models of the theories of valued algebraically closed fields and convexly valued real closed fields, their reducts to the pure field or ordered field language respectively, and expansions of these by predicates which are definable in the valued field. We show that, in terms of definability, there is no structure properly between the pure (ordered) field and the valued field. Our results are analogous to several other definability results for reducts of algebraically closed and real closed fields; see [9], [10], [11] and [12]. Throughout this paper, definable will mean definable with parameters.

Theorem A. Let ℱ = (F, +, ×, V) be a valued, algebraically closed field, where V denotes the valuation ring. Let A be a subset ofFndefinable in ℱv. Then either A is definable in ℱ = (F, +, ×) or V is definable in.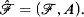

Theorem B. Let ℛv = (R, <, +, ×, V) be a convexly valued real closed field, where V denotes the valuation ring. Let Abe a subset ofRndefinable in ℛv. Then either A is definable in ℛ = (R, <, +, ×) or V is definable in.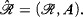

The proofs of Theorems A and B are quite similar. Both ℱv and ℛv admit quantifier elimination if we adjoin a definable binary predicate Div (interpreted by Div(x, y) if and only if v(x) ≤ v(y)). This is proved in [14] (extending [13]) in the algebraically closed case, and in [4] in the real closed case. We show by direct combinatorial arguments that if the valuation is not definable then the expanded structure is strongly minimal or o-minimal respectively. Then we call on known results about strongly minimal and o-minimal fields to show that the expansion is not proper.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 2 , June 1998 , pp. 739 - 743
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bélair, L., Anneaux p-adiquement clos et anneaux defonctions definissables, this Journal, vol. 56 (1991), pp. 539–553.Google Scholar
[2] Birch, A. J., Burns, R. G., Macdonald, S. O., and Neumann, P. M., On the orbit-sizes of permutation groups containing elements separating finite sets, Bulletin of the Australian Mathematical Society, vol. 14 (1976), pp. 7–10.Google Scholar
[3] Cameron, P. J., Oligomorphic permutation groups, Cambridge University Press, Cambridge, 1990.Google Scholar
[4] Cherlin, G. and Dickmann, M., Real closed rings II, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 213–231.Google Scholar
[5] Haskell, D. and Macpherson, H. D., Cell decompositions of C-minimal structures, Annals of Pure and Applied Logic, vol. 66 (1994), pp. 113–162.Google Scholar
[6] Holly, J. E., Canonical forms for definable subsets of algebraically closed and real closed valued fields, this Journal, vol. 60 (1995), pp. 843–860.Google Scholar
[7] Hrushovski, E., Strongly minimal expansions of algebraically closed fields, Israel Journal of Mathematics, vol. 79 (1992), pp. 129–151.Google Scholar
[8] Macpherson, H. D. and Steinhorn, C., On variants ofo-minimality, Annals of Pure and Applied Logic, vol. 79 (1996), pp. 165–209.Google Scholar
[9] Marker, D., Semialgebraic expansions of C, Transactions of the American Mathematical Society, vol. 320 (1990), pp. 581–592.Google Scholar
[10] Marker, D., Peterzil, Y., and Pillay, A., Additive reducts of real closed fields, this Journal, vol. 57 (1992), pp. 109–117.Google Scholar
[11] Pillay, A., Scowcroft, P., and Steinhorn, C., Between groups and rings, Rocky Mountain Journal of Mathematics, vol. 19 (1989), pp. 871–885.Google Scholar
[12] Rabinovich, E. D., Definability of a field in sufficiently rich incidence systems Maths Lecture Notes 14, Queen Mary and Westfield College.Google Scholar
[13] Robinson, A., Complete theories, North Holland, Amsterdam, 1956.Google Scholar
[14] Weispfenning, V., Quantifier elimination and decision procedures for valued fields, Models and sets (Müller, G. H. and Richter, M. M., editors), Lecture Notes in Mathematics, no. 1103, Springer-Verlag, Berlin, 1984, pp. 419–472.Google Scholar