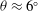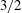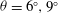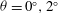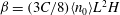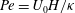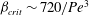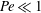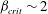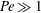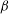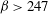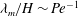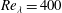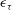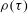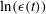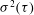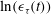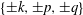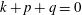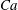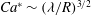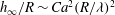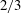Rapids
A reciprocal theorem for Marangoni propulsion
-
- Published online by Cambridge University Press:
- 11 February 2014, R4
-
- Article
- Export citation
Papers
Non-Boussinesq gravity currents propagating on different bottom slopes
-
- Published online by Cambridge University Press:
- 13 February 2014, pp. 658-680
-
- Article
- Export citation
Instability of an inhomogeneous bacterial suspension subjected to a chemo-attractant gradient
-
- Published online by Cambridge University Press:
- 17 February 2014, pp. 619-657
-
- Article
- Export citation
Adjoint-based control of loud events in a turbulent jet
-
- Published online by Cambridge University Press:
- 07 February 2014, pp. 28-59
-
- Article
- Export citation
Stability analysis for the onset of thermoacoustic oscillations in a gas-filled looped tube
-
- Published online by Cambridge University Press:
- 13 February 2014, pp. 585-618
-
- Article
- Export citation
The role of surfactants on the mechanism of the long-wave instability in liquid film flows
-
- Published online by Cambridge University Press:
- 12 February 2014, pp. 139-155
-
- Article
- Export citation
The wake of a two-dimensional ship in the low-speed limit: results for multi-cornered hulls
-
- Published online by Cambridge University Press:
- 17 February 2014, pp. 492-513
-
- Article
- Export citation
Rapids
Lagrangian cascade in three-dimensional homogeneous and isotropic turbulence
-
- Published online by Cambridge University Press:
- 12 February 2014, R2
-
- Article
- Export citation
Papers
Effects of surface corrugation on the stability of a zero-pressure-gradient boundary layer
-
- Published online by Cambridge University Press:
- 12 February 2014, pp. 228-251
-
- Article
- Export citation
Transport mechanisms of the turbulent energy cascade in upward/downward bubbly flows
-
- Published online by Cambridge University Press:
- 13 February 2014, pp. 514-542
-
- Article
- Export citation
Flow of a falling liquid curtain into a pool
-
- Published online by Cambridge University Press:
- 17 February 2014, pp. 350-376
-
- Article
- Export citation
Droplet–turbulence interaction in a confined polydispersed spray: effect of droplet size and flow length scales on spatial droplet–gas velocity correlations
-
- Published online by Cambridge University Press:
- 07 February 2014, pp. 98-138
-
- Article
- Export citation
Rapids
Note on the triad interactions of homogeneous turbulence
-
- Published online by Cambridge University Press:
- 21 February 2014, R3
-
- Article
- Export citation
Rotne–Prager–Yamakawa approximation for different-sized particles in application to macromolecular bead models
-
- Published online by Cambridge University Press:
- 11 February 2014, R5
-
- Article
- Export citation
Papers
Linearized oscillations of a vortex column: the singular eigenfunctions
-
- Published online by Cambridge University Press:
- 20 February 2014, pp. 404-460
-
- Article
- Export citation
Surface slopes, velocity profiles and fluid pressure in coarse-grained debris flows saturated with water and mud
-
- Published online by Cambridge University Press:
- 17 February 2014, pp. 377-403
-
- Article
- Export citation
Streak instabilities in boundary layers beneath free-stream turbulence
-
- Published online by Cambridge University Press:
- 13 February 2014, pp. 280-315
-
- Article
- Export citation
Non-classical gas dynamics of vapour mixtures
-
- Published online by Cambridge University Press:
- 13 February 2014, pp. 681-701
-
- Article
- Export citation
Instantaneous pressure measurements on a spherical grain under threshold flow conditions
-
- Published online by Cambridge University Press:
- 07 February 2014, pp. 60-97
-
- Article
- Export citation
Breakdown of the Bretherton law due to wall slippage
-
- Published online by Cambridge University Press:
- 07 February 2014, pp. 200-227
-
- Article
- Export citation