Clusters of inertial particles in turbulence are usually identified from the spatial coherence of the particle concentration field, neglecting their temporal persistence. The latter is in fact essential to the ability of the particles to interact with each other and to modify the flow. Here, we leverage simulations of homogeneous isotropic turbulence laden with small heavy particles and develop a Lagrangian framework to follow them before, during and after their time as part of a coherent cluster. We define a criterion to establish whether a cluster survives over successive time steps, and use it to characterize its lifetime. We find that cluster lives have typical durations of a few Kolmogorov time scales, with positive correlation between cluster size and lifetime. Increasing inertia and gravitational settling both lead to longer lifetimes. Small clusters emerge from the coagulation of non-clustered particles, quickly followed by disintegration into prevalently non-clustered particles. By contrast, large clusters result from the recombination of other large clusters. The birth of a cluster is preceded by an exponential contraction of the particle cloud, and its death coincides with the beginning of a slower exponential expansion, The contraction is simultaneous to a decline in the local small-scale turbulence activity, while the expansion is accompanied by its recovery. Therefore, during their lifetime, the clusters experience lower-than-average enstrophy and strain rate in the fluid. This relatively quiescent state of the flow is thus a necessary condition for the cluster survival, at least in the considered range of turbulence intensity and particle inertia.

Kessler (Nature, vol. 313, 1985, pp. 218–220) first showed that plume-like structures spontaneously appear from both stationary and flowing suspensions of gyrotactic microswimmers in a vertical pipe. Recently, it has been shown that there exist multiple steady, axisymmetric and axially uniform solutions to such a system (Bees & Croze, Proc. R. Soc. A, vol. 466, 2010, pp. 2057–2077). In the present study, we generalise this finding by reporting that a countably infinite number of such solutions emerge as the Richardson number increases. Linear stability, weakly nonlinear and fully nonlinear analyses are performed, revealing that each of the solutions arises from the destabilisation of a uniform suspension. The countability of the solutions is due to the finite flow domain, while the transcritical nature of the bifurcation is because of the cylindrical geometry, which breaks the horizontal symmetry of the system. It is further shown that there exists a maximum threshold of achievable downward flow rate for each solution if the flow is to remain steady, as varying the pressure gradient can no longer increase the flow rate from the solution. All of the solutions found are unstable, except for the one arising at the lowest Richardson number, implying that they would play a role in the transient dynamics in the route from a uniform suspension to the fully developed gyrotactic pattern.

The flow past a fixed rigid cylinder becomes unsteady beyond a critical Reynolds number close to $47$, based on the body diameter and inflow velocity. The present paper explores numerically the vortex-induced vibrations (VIV) that may develop for a flexible cylinder at subcritical Reynolds number ($Re$), i.e. for $Re<47$. Flexible-cylinder VIV are found to occur down to $Re\approx 20$, as previously reported for elastically mounted rigid cylinders. A detailed analysis is carried out for $Re=25$, in two steps: the system behaviour is examined from the emergence of VIV to the excitation of the first structural modes; and then focus is placed on higher-mode responses. In all cases, a single vibration frequency is excited in each direction. The cross-flow and in-line responses exhibit contrasting magnitudes (peak amplitudes of $0.35$ versus $0.01$ diameters), as well as distinct symmetry properties and evolutions (e.g. standing/travelling waves). The flow, unsteady once the cylinder vibrates, is found to be temporally and spatially locked with body motion. The synchronization with the cross-flow standing-wave responses is accompanied by the formation of cellular wake patterns, regardless of the modes involved in the vibrations. Body trajectory varies along the span, but dominant orbits can be identified. Despite the low amplitudes of the in-line responses, connections are uncovered between orbit orientation and flow–structure energy transfer, with different trends in each direction.

The theory of Kolmogorov, enunciated for very large Reynolds numbers, has progressively been shown to be inoperative for characterizing flows of practical relevance. Yet, in a recent study by Alves Portela et al. (J. Fluid Mech., vol. 896, 2020, A16), the turbulence statistics in the very near wake of a square prism at modest Reynolds numbers, reveal a significant portion of scales complying with a cascade of Kolmogorov type. By resorting to a generalized version of the Kármán–Howarth–Kolmogorov equation, this intriguing observation is shown to be an illusion, hiding a measurable influence of coherent structures and statistical inhomogeneity. This striking conclusion highlights that a complete statistical theory of turbulence cannot dispense with the influence of large scales, possibly coherent, motions.

Shock-wave reflection over concave surfaces poses a difficulty in its analysis due to the unsteady nature of the reflection process and the occurrence of various types of Mach reflections caused by it. In a pseudo-steady flow, the reflection's configuration is self-similar since the shock wave reflects over a surface with constant inclination. The unsteady Mach reflection introduces an additional complexity as it is affected by the changing inclination of the surface, forcing the reflection to continuously adjust itself to the varying boundary condition. In this study, validated simulations of Mach reflection (MR) over cylindrical concave surfaces with different radii were performed for three inviscid perfect gases with moderate incident shock Mach numbers (Ms) ranging from 1.3 to 1.5. The reflection was investigated up to the point of transition from MR to transitioned regular reflection. A similar behaviour of the configuration and evolution of the Mach stem was observed, one that is independent of the surface radius and type of gas. With regards to different gases, the speed of sound a0 is a dominant factor since it dictates the propagation of wall disturbances. A universal condition of the rate of surface change was found, accounting for different radii, different gases and Ms variation. Analysis based on shock dynamics is employed to explain how disturbances caused by surface variations play a significant role in the behaviour of the reflection. This method successfully supports the similarity that was demonstrated and facilitates a more informed perception of the MR process.

In this paper, we theoretically investigate the migration of a surfactant covered droplet in a Poiseuille flow by including the surface viscosities of the droplet. We employ a regular perturbation expansion for low surface Péclet numbers and solve the problem up to a second-order approximation. We represent the drop surface as a two-dimensional homogeneous fluid using the Bousinessq–Scriven law and employ Lamb's general solution to represent the velocity fields inside and outside the droplet. We obtain an expression for the cross-stream migration velocity of the droplet, where the surface viscosities are captured by the Bousinessq numbers for surface shear and surface dilatation. We elucidate the influence of the surface viscosities on the migration characteristics of the droplet and the surfactant redistribution on the droplet surface. Our study sheds light on the importance of including the droplet surface viscosities to accurately predict the migration characteristics of the droplet.

The convergent Richtmyer–Meshkov instability (RMI) of an $\textrm {SF}_6$ layer with a uniform outer surface and a sinusoidal inner surface surrounded by air (generated by a novel soap film technique) is studied in a semiannular convergent shock tube using high-speed schlieren photography. The outer interface initially suffers only a slight deformation over a long period of time, but distorts quickly at late stages when the inner interface is close to it and produces strong coupling effects. The development of the inner interface can be divided into three stages. At stage I, the interface amplitude first drops suddenly to a lower value due to shock compression, then decreases gradually to zero (phase reversal) and later increases sustainedly in the negative direction. After the reshock (stage II), the perturbation amplitude exhibits long-term quasi-linear growth with time. The quasi-linear growth rate depends weakly on the pre-reshock amplitude and wavelength, but strongly on the pre-reshock growth rate. An empirical model for the growth of convergent RMI under reshock is proposed, which reasonably predicts the present results and those in the literature. At stage III, the perturbation growth is promoted by the Rayleigh–Taylor instability caused by a rarefaction wave reflected from the outer interface. It is found that both the Rayleigh–Taylor effect and the interface coupling depend heavily on the layer thickness. Therefore, controlling the layer thickness is an effective way to modulate the late-stage instability growth, which may be useful for the target design.

We examine the effect of gravity and (rotational) inertia on the inertial focusing of spherical non-neutrally buoyant particles suspended in flow through curved microfluidic ducts. In the neutrally buoyant case, examined in Harding et al. (J. Fluid Mech., vol. 875, 2019, pp. 1–43), the gravitational contribution to the force on the particle is exactly zero and the net effect of centrifugal and centripetal forces (due to the motion around the curved duct) is negligible. Inertial lift force and drag from the secondary fluid flow vortices interact and lead to focusing behaviour which is sensitive to the bend radius of the device and the particle size (each measured relative to the height of the cross-section). In the case of non-neutrally buoyant particles the behaviour becomes more complex with the two additional perturbing forces. The gravitational force, relative to the inertial lift force, scales with the inverse square of the flow velocity, making it a potentially important factor for devices operating at low flow rates with a suspension of non-neutrally buoyant particles. In contrast, the net centripetal/centrifugal force scales with the inverse of the bend radius, similar to the drag force from the secondary flow. We examine how these forces perturb the stable equilibria within the cross-sectional plane to which neutrally buoyant particles ultimately migrate.

We study the influence of a membrane filter's internal pore structure on its flow and adsorptive fouling behaviour. Membrane performance is measured via (1) comparison between volumetric flow rate and throughput during filtration and (2) control of concentration of foulants at membrane pore outlets. Taking both measures into account, we address the merits and drawbacks of selected membrane pore structures. We first model layered planar membrane structures with intra-layer pore connections, and present comparisons between non-connected and connected structures. Our model predicts that membrane filters with connected pore structures lead to higher total volumetric throughput than those with non-connected structures, over the filter lifetime. We also provide a sufficient criterion for the concentration of particles escaping the filter to achieve a maximum in time (indicative of a membrane filter whose particle retention capability can deteriorate). Additionally, we find that the influence of intra-layer heterogeneity in pore-size distribution on filter performance depends on the connectivity properties of the pores.

An experimental study of particle–vortex interactions has been undertaken in suspensions with volume fractions up to $\Phi =20\,\%$. Time-resolved particle image velocimetry measurements using a refractive index matching technique were performed to characterize the formation and evolution of vortex rings in both unconfined and confined configurations. It is shown that vortex rings in dense suspensions are more diffuse, which results in larger vortex cores and lower maximum vorticity. Furthermore, these vortex rings remain stable during their evolution, whereby the primary vortex breakdown and the formation of secondary vortices are inhibited. Although similar to vortex rings generated at lower Reynolds numbers in pure water, further results demonstrate that the vortex-ring circulation and non-dimensional vortex-core radius in dense suspensions remain higher than those in pure water at the same equivalent Reynolds number. Thus, the modification of vortex-ring behaviour in dense suspensions cannot be described solely through a variation in the effective viscosity. Finally, unlike in pure water, the confinement does not impact the non-dimensional vortex-core radius, vortex-ring circulation and maximum vorticity in dense suspensions. This unusual result demonstrates that the dynamics of vortex rings in dense suspensions are strongly insensitive to the effect of confinement.

Wind generated near-inertial waves are ubiquitous in the upper ocean. An improved understanding of near-inertial wave dynamics following their excitation in the ocean and their subsequent interaction with mesoscale geostrophic balanced flows is key to decoding oceanic energy flow pathways. In this regard, multiple oceanic data sets accumulated over the past few decades reveal that the relative strength of near-inertial waves and geostrophic balanced eddy fields is highly variable, both geographically and seasonally. Inspired by these observations, we investigate turbulent interactions and energy exchanges between near-inertial waves and balanced flows using freely evolving numerical simulations of the non-hydrostatic Boussinesq equations. We find accelerated vertical propagation and dissipation of the waves in regimes where balanced and wave fields have comparable strengths. In such regimes we also find that near-inertial waves directly extract energy from balanced flows, with $O(10\, \%)$ being the amount of balanced energy loss. In contrast, we find that near-inertial waves transfer energy to balanced flows in regimes where balance-to-wave energy ratio is small, with the gain in balanced energy being dependent on the relative strength of waves. Furthermore, these regimes are characterized by relatively weaker vertical propagation and dissipation of the near-inertial wave field. One of the key outcomes of this study is the demonstration of the lack of a unique direction for near-inertial wave-balanced flow energy transfers. Depending on the balance-to-wave energy ratio, near-inertial waves can act as an energy sink or energy source for the geostrophic balanced flow.

As two spherical gas bubbles of radii 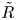$\tilde {R}$ are brought together inside a liquid of density 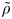$\tilde {\rho }$, viscosity $\tilde {\mu }$ and surface tension 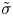$\tilde {\sigma }$, the liquid sheet separating them drains, thins and ultimately ruptures. The instant and location at which the bubbles make contact, and whereby a circular hole of vanishingly small radius is formed in the thin sheet, represent the occurrence of a finite-time singularity. The large curvature near the edge of the sheet where the hole has just formed, and where the two bubbles are now connected via a microscopic gas bridge, drives liquid to flow radially outward, causing the sheet to retract and the radius of the hole 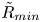$\tilde {R}_{min}$ to increase with time. Recent work in this area has uncovered self-similarity and universal scaling regimes when two bubbles coalesce in a Newtonian fluid. Motivated by applications in which the exterior is a deformation-rate-thinning, power-law fluid, recent studies on bubble coalescence in Newtonian fluids are extended to coalescence in power-law fluids. 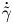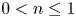In such fluids, viscosity decreases with deformation rate $\dot {\tilde {\gamma }}$ raised to the $n - 1$ power where $0 < n \le 1$ ($n = 1$ for a Newtonian fluid). Attention is focused here on power-law fluids that are slightly viscous at zero deformation rate, i.e. when the Ohnesorge number 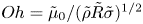$Oh = \tilde {\mu }_{0}/(\tilde {\rho } \tilde {R} \tilde {\sigma })^{1/2}$ is small (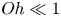$Oh \ll 1$) and where 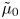$\tilde {\mu }_0$ is the zero-deformation-rate viscosity. A combination of thin-film theory and three-dimensional, axisymmetric computations is used to probe the dynamics in the aftermath of the singularity. Heretofore unexplored regimes are uncovered, and criteria are developed for transitions between different regimes. The existence of a truly inviscid regime, predicted long ago by Keller (Phys. Fluids, vol. 26, 1983, pp. 3451–3453) and which comes into play as a purely geometrical limit of the free-surface shape, is also reported. New insights are presented on the much studied Newtonian limit beyond the initial regime reported by Munro et al. (J. Fluid Mech., vol. 773, 2015, R3). The paper concludes with a phase diagram in 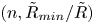$(n, \tilde {R}_{min}/\tilde {R})$-space, where the index 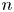$n$ characterizes the fluid and 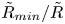$\tilde {R}_{min}/\tilde {R}$ the extent of coalescence, that highlights the various regimes and transitions between them.

We perform inviscid and viscous, global, linear stability analyses of vortex rings which are compared with asymptotic theories and numerical simulations. We find growth rates of rings to be very sensitive to the details of vorticity distribution, in a way not accounted for in asymptotic theories, clearly demonstrated in our analyses of equilibrated rings–ring base flows initially obtained from Gaussian rings evolved to a quasi-steady state before any instabilities set in. Such equilibrated rings with the same $\epsilon = a/R$, the ratio of core radius $a$ to ring radius $R$, but evolved with different viscosities, have inviscid growth rates differing by up to 9 %, though the differences in vorticity at any point are small. In contrast, the growth rates of rings with a Gaussian vorticity distribution are found to be up to 33 % smaller than the inviscid asymptotic theories over $0.4 > \epsilon > 0.05$. We attribute these differences to the nature of velocity fields at $O(\epsilon ^2)$, between equilibrated and Gaussian rings, where the former shows a good quantitative match with the asymptotic theories. Additionally, there are some differences with previous direct numerical simulations (DNS), but in very close quantitative agreement with our DNS results. Our calculations provide a new relation capturing the near-linear dependence of growth rates on the reciprocal of a strain rate-based Reynolds number $\widehat Re$. Importantly, our equilibrated ring calculations do tend to the inviscid limit of asymptotic theories, once corrections for ring radius evolution and equilibrated distribution are imposed, unlike for Gaussian rings.

The paper presents results of numerical simulations of a dissolved substance diffusing out of a liquid film in a two-dimensional, gravity-driven laminar flow down a vertical solid plane. The fluid mechanic problem is solved separately subject to periodicity conditions in the flow direction. After steady-state is reached, up to a hundred copies of the calculated wave and associated flow fields are efficiently ‘glued’ together to generate a long computational domain for the diffusion process which is solved as an initial-value problem. This approach renders it possible to follow the diffusion process over a long distance and to elucidate its various stages. It is found that large and small waves, with a maximum liquid velocity larger or smaller than the wave speed, respectively, behave differently. For the latter, the Sherwood number reaches an asymptotic value by the time the film still contains a significant amount of solute. From this point on, the mass transfer is very similar to that of a flat film with a smaller thickness (quantified in this paper). For large waves, the contributions of the various parts of the wave – main crest, capillary waves, nearly flat substrate – evolve differently with time and conditions and may negatively affect the mass transfer process if they get out of balance. Thus, the presence of recirculation is, in and by itself, insufficient to judge the mass transfer performance of a falling film.

Previous experimental (Kühnen et al., Flow Turb. Combust., vol. 100, 2018, pp. 919–943) and numerical (Marensi et al., J. Fluid Mech., vol. 863, 2019, pp. 850–875) studies have demonstrated that a streamwise-localised baffle can fully relaminarise pipe flow turbulence at Reynolds numbers of $O(10^4)$. Optimising the design of the baffle involves tackling a complicated variational problem built around time stepping turbulent solutions of the Navier–Stokes equations which is difficult to solve. Here instead, we investigate a much simpler ‘spectral’ approach based upon maximising the energy stability of the baffle-modified laminar flow. The ensuing optimal problem has much in common with the variational procedure to derive an upper bound on the energy dissipation rate in turbulent flows (e.g. Plasting & Kerswell, J. Fluid Mech., vol. 477, 2003, pp. 363–379) so well-honed techniques developed there can be used to solve the problem here. The baffle is modelled by a linear drag force $-F(\boldsymbol {x}) \boldsymbol {u}$ (with $F(\boldsymbol {x}) \ge 0 \ \forall \boldsymbol {x}$) where the extent of the baffle is constrained by an $L_{\alpha }$ norm with various choices explored in the range $1 \leq \alpha \leq 2$. An asymptotic analysis demonstrates that the optimal baffle is always axisymmetric and streamwise independent, retaining just radial dependence. The optimal baffle which emerges in all cases has a similar structure to that found to work in experiments: the baffle retards the flow in the pipe centre causing the flow to become faster near the wall thereby reducing the turbulent shear there. Numerical simulations demonstrate that the designed baffle can relaminarise turbulence efficiently at moderate Reynolds numbers ($Re \le 3500$), and an energy saving regime has been identified. Direct numerical simulation at $Re=2400$ also demonstrates that the drag reduction can be realised by truncating the energy-stability-designed baffle to finite length.

Due to triboelectric charging, the solid phase in gas–particle flows can become electrically charged, inducing an electrical interaction among all the particles in the system. Because this force decays rapidly, many of the current models neglect the contribution of this electrostatic interaction. In this work, an Eulerian particle model for gas–particle flow is proposed in order to take into consideration the electrostatic interaction among the particles. The kinetic theory of granular flows is used to derive the transport equation for the mean particle electric charge. The collision integrals are closed without presuming the form of the electric part for the particle probability density function. A linear model for the mean electric charge conditioned by the instantaneous particle velocity is proposed to account for the charge–velocity correlation. First, a transport equation is written for the charge–velocity correlation. Then, a gradient dispersion model is derived from this equation by using some simplifying hypotheses. The model is tested in a three-dimensional periodic box. The results show that the dispersion phenomenon has two contributions: a kinetic contribution due to the electric charge transport by the random motion of particles and a collisional contribution due to the electric charge transfer during particle–particle collisions. Another phenomenon that contributes to the mean electric charge transport is a triboelectrical current density due to the tribocharging effect by particle–particle collisions in the presence of a global electric field. The corresponding electric charge flux is written as equal to the product of the electric field by a triboconductivity coefficient.

Measurements of wall-pressure and velocity fluctuations are performed in a family of three incompressible, pressure-induced, turbulent separation bubbles (TSBs) of varying sizes, with an emphasis on the energetic low and medium frequencies. In all three cases the streamwise distribution of wall-pressure fluctuations shows a bi-modal character, with a first local maximum close to the position of maximum adverse pressure gradient and a second local maximum at the very end of the region of intermittent back flow. The first maximum is shown to be caused by the superposition of two separate phenomena occurring at approximately the same streamwise position: first, the pressure signature of a low-frequency contraction and expansion (breathing) of the TSBs, whose amplitude is shown to increase with the size of the separation bubble, and second, the effect of the adverse pressure gradient on the turbulent structures responsible for the pressure fluctuations in the attached boundary layer. The second maximum of the wall-pressure fluctuation coefficient also increases with the size of the TSB and is associated with the convection of large structures within the shear layer. Possible scaling laws are examined to show that both the local maximum Reynolds shear stress ${-\rho \overline {u'v'}_{max}}$ and the local maximum wall-normal stress ${\rho \overline {v'v'}_{max}}$ are adequate to scale the pressure fluctuations along the TSBs, with a better match when low frequencies are removed. Furthermore, a comparison with existing data from the literature illustrates the effects of Reynolds number and TSB size on the wall-pressure and velocity fluctuations. Finally, measurements in the spanwise direction demonstrate that, although corner effects strongly distort the average flow, the scaling of wall-pressure fluctuations with the turbulent stresses remains relatively unaffected. The present results provide new insights into the unsteady character of pressure-induced turbulent separation bubbles and their associated wall-pressure fluctuations.

This study attempts to quantify and explain the systematic weakening of internal gravity waves in fingering and diffusive thermohaline staircases. The interaction between waves and staircases is explored using a combination of direct numerical simulations (DNS) and an asymptotic multiscale model. The multiscale theory makes it possible to express the wave decay rate $({\lambda _d})$ as a function of its wavenumbers and staircase parameters. We find that the decay rates in fully developed staircases greatly exceed values that can be directly attributed to molecular dissipation. They rapidly increase with increasing wavenumbers, both vertical and horizontal. At the same time, ${\lambda _d}$ is only weakly dependent on the thickness of layers in the staircase, the overall density ratio and the diffusivity ratio. The proposed physical mechanism of attenuation emphasizes the significance of eddy diffusion of temperature and salinity, whereas eddy viscosity plays a secondary role in damping internal waves. The asymptotic model is successfully validated by the DNS performed in numerically accessible regimes. We also discuss potential implications of staircase-induced suppression for diapycnal mixing by overturning internal waves in the ocean.

An electrokinetic model for a surfactant-stabilized nano-drop under oscillatory forcing is solved. This generalizes a model for which an analytical solution was recently proposed for large, highly charged drops. Calculations of the dynamic electrophoretic mobility and the accompanying electrostatic polarization for a single drop provide a theoretical foundation for interpreting electrokinetic sonic amplitude and complex-conductivity spectra for dilute surfactant-stabilized oil-in-water emulsions and bubbly liquids. The model is distinguished from earlier models by accounting for the internal fluid and interfacial dynamics at finite frequencies (${\sim }10^3\text {--}10^7\ \textrm {Hz}$). This dynamics accounts for the electro-migration, diffusion and advection of surfactant ions on the interface, and exchange of these ions with the immediately adjacent electrolyte. Surface gradients induce Marangoni stresses, which couple to the electrical and hydrodynamic stresses, modulating the magnitude and phase of the drop velocity and electrostatic polarization induced by the electric field. Of particular interest, for sodium dodecyl sulphate stabilized oil-in-water drops, is how the high surface-charge density manifests in a breakdown of the Smoluchowski-slip approximation, even for drops with very thin diffuse layers. More generally, the model furnishes dynamic mobilities for drops with arbitrary size and charge, thus permitting appropriate averaging for polydisperse systems. Such calculations may help to resolve long-standing challenges and controversy with regards to the surface-charge density of nano-drops and their macro-scale counterparts, and may pave the way to quantitative interpretations of more complex dynamic interfacial rheology and exchange kinetics, e.g. for Pickering emulsions.

Ureteroscopy is a minimally invasive surgical procedure for the removal of kidney stones. A ureteroscope, containing a hollow, cylindrical working channel, is inserted into the patient's kidney. The renal space proximal to the scope tip is irrigated, to clear stone particles and debris, with a saline solution that flows in through the working channel. We consider the fluid dynamics of irrigation fluid within the renal pelvis, resulting from the emerging jet through the working channel and return flow through an access sheath. Representing the renal pelvis as a two-dimensional rectangular cavity, we investigate the effects of flow rate and cavity size on flow structure and subsequent clearance time of debris. Fluid flow is modelled with the steady incompressible Navier–Stokes equations, with an imposed Poiseuille profile at the inlet boundary to model the jet of saline, and zero-stress conditions on the outlets. The resulting flow patterns in the cavity contain multiple vortical structures. We demonstrate the existence of multiple solutions dependent on the Reynolds number of the flow and the aspect ratio of the cavity using complementary numerical simulations and particle image velocimetry experiments. The clearance of an initial debris cloud is simulated via solutions to an advection–diffusion equation and we characterise the effects of the initial position of the debris cloud within the vortical flow and the Péclet number on clearance time. With only weak diffusion, debris that initiates within closed streamlines can become trapped. We discuss a flow manipulation strategy to extract debris from vortices and decrease washout time.