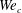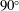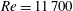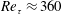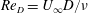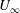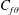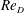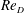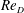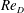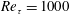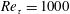JFM Papers
Evolution and stationarity of liquid toroidal drop in compressional Stokes flow
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 1-23
-
- Article
- Export citation
Non-isolated drop impact on surfaces
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 24-44
-
- Article
- Export citation
Turbulent flows over superhydrophobic surfaces: flow-induced capillary waves, and robustness of air–water interfaces
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 45-85
-
- Article
- Export citation
The three-dimensional structure of swirl-switching in bent pipe flow
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 86-101
-
- Article
- Export citation
Premixed turbulent flame speed in an oscillating disturbance field
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 102-130
-
- Article
- Export citation
The set-down and set-up of directionally spread and crossing surface gravity wave groups
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 131-169
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of temperature gradient on the cross-stream migration of a surfactant-laden droplet in Poiseuille flow
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 170-216
-
- Article
- Export citation
Turbulent boundary layers absent mean shear
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 217-251
-
- Article
- Export citation
Trajectory of a model bacterium
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 252-270
-
- Article
- Export citation
Characteristics of the turbulent energy dissipation rate in a cylinder wake
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 271-300
-
- Article
- Export citation
Determination of the bottom deformation from space- and time-resolved water wave measurements
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 301-326
-
- Article
- Export citation
Large-eddy simulation of flow over a grooved cylinder up to transcritical Reynolds numbers
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 327-362
-
- Article
- Export citation
Pore-scale modelling of Ostwald ripening
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 363-392
-
- Article
-
- You have access
- HTML
- Export citation
Dynamics and structure of an apolar active suspension in an annulus
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 393-405
-
- Article
- Export citation
Scaling law for the lift force of autorotating falling seeds at terminal velocity
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 406-420
-
- Article
- Export citation
DNS of a turbulent Couette flow at constant wall transpiration up to
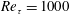 $Re_{\unicode[STIX]{x1D70F}}=1000$
$Re_{\unicode[STIX]{x1D70F}}=1000$
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 421-443
-
- Article
- Export citation
Oscillations of confined fibres transported in microchannels
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 444-470
-
- Article
- Export citation
Temporal acceleration of a turbulent channel flow
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 471-490
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixed insulating and conducting thermal boundary conditions in Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 491-511
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Water entry of a wedge with rolled-up vortex sheet
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 512-539
-
- Article
- Export citation