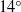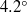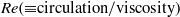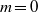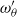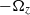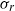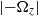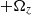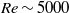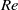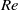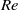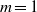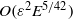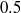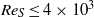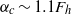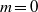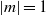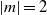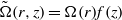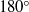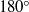Focus on Fluids
Natural logarithms
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 5-38
-
- Article
- Export citation
Self-limiting and regenerative dynamics of perturbation growth on a vortex column
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 39-88
-
- Article
- Export citation
The role of large-scale vortical structures in transient convective heat transfer augmentation
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 89-115
-
- Article
- Export citation
Initial growth of a disturbance in a boundary layer influenced by a circular cylinder wake
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 116-130
-
- Article
- Export citation
Nonlinear vorticity-banding instability in granular plane Couette flow: higher-order Landau coefficients, bistability and the bifurcation scenario
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 131-180
-
- Article
- Export citation
Libration-induced mean flow in a spherical shell
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 181-209
-
- Article
- Export citation
The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 210-245
-
- Article
- Export citation
Stability of a liquid ring on a substrate
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 246-279
-
- Article
- Export citation
Phase-averaged equation for water waves
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 280-303
-
- Article
- Export citation
Experimental evidence for a short-wave global mode in film flow along periodic corrugations
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 304-320
-
- Article
- Export citation
Skin friction on a moving wall and its implications for swimming animals
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 321-346
-
- Article
- Export citation
Lattice ellipsoidal statistical BGK model for thermal non-equilibrium flows
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 347-370
-
- Article
- Export citation
Nonlinear long waves over a muddy beach
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 371-397
-
- Article
- Export citation
Direct numerical simulations of local and global torque in Taylor–Couette flow up to Re = 30 000
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 398-427
-
- Article
- Export citation
Longwave Marangoni convection in a surfactant solution between poorly conducting boundaries
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 428-456
-
- Article
- Export citation
Stability of a Gaussian pancake vortex in a stratified fluid
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 457-480
-
- Article
- Export citation
Contact lines with a
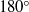 $18{0}^{\circ } $ contact angle
$18{0}^{\circ } $ contact angle
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 481-506
-
- Article
- Export citation
A simple constitutive model for predicting the pressure histories developed behind rigid porous media impinged by shock waves
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 507-523
-
- Article
- Export citation
Dispersive shock waves in viscously deformable media
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 524-557
-
- Article
- Export citation