Research Article
Stochastic Epidemic Models in Structured Populations Featuring Dynamic Vaccination and Isolation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 571-585
-
- Article
-
- You have access
- Export citation
A Stochastic Maximin Fixed-Point Equation Related to Game Tree Evaluation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 586-606
-
- Article
-
- You have access
- Export citation
Characterizations of Conditional Comonotonicity
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 607-617
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of a Generalized TCP Congestion Avoidance Algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 618-635
-
- Article
-
- You have access
- Export citation
Stability of Processor Sharing Networks with Simultaneous Resource Requirements
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 636-651
-
- Article
-
- You have access
- Export citation
Strong Convergence for URN Models with Reducible Replacement Policy
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 652-660
-
- Article
-
- You have access
- Export citation
Generalized Pólya urn Designs with Null Balance
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 661-669
-
- Article
-
- You have access
- Export citation
Asymptotic Expansions for Distributions of Compound Sums of Random Variables with Rapidly Varying Subexponential Distribution
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 670-684
-
- Article
-
- You have access
- Export citation
Ruin Probability for the Integrated Gaussian Process with Force of Interest
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 685-694
-
- Article
-
- You have access
- Export citation
The Joint Density of the Surplus Before and After Ruin in the Sparre Andersen Model
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 695-712
-
- Article
-
- You have access
- Export citation
Discounted Optimal Stopping for Maxima of Some Jump-Diffusion Processes
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-731
-
- Article
-
- You have access
- Export citation
A Lévy Process whose Jumps are Dragged by a Spherical Dynamical System
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 732-741
-
- Article
-
- You have access
- Export citation
Optimal Smooth Portfolio Selection for an Insider
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 742-752
-
- Article
-
- You have access
- Export citation
The Critical Galton-Watson Process Without Further Power Moments
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 753-769
-
- Article
-
- You have access
- Export citation
Voter Model and Biased Voter Model in Heterogeneous Environments
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 770-787
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of k-Word Matches Between two Uniformly Distributed Sequences
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 788-805
-
- Article
-
- You have access
- Export citation
Integration by Parts for Point Processes and Monte Carlo Estimation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 806-823
-
- Article
-
- You have access
- Export citation
Counts of Failure Strings in Certain Bernoulli Sequences
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 824-830
-
- Article
-
- You have access
- Export citation
Explicit Optimal Strategy for the Vardi Casino with Limited Playing Time
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 831-837
-
- Article
-
- You have access
- Export citation
A Note on Planar Random Motion at Finite Speed
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 838-842
-
- Article
-
- You have access
- Export citation



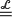 ξ max
ξ max