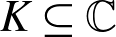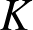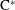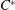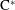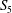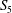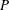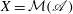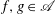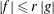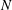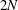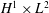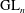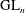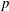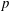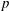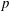Algebraic and Complex Geometry
Research Article
MULTIPLICATIVE SUB-HODGE STRUCTURES OF CONJUGATE VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2014, e1
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
A NONSEPARABLE AMENABLE OPERATOR ALGEBRA WHICH IS NOT ISOMORPHIC TO A
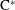 $C^*$-ALGEBRA
$C^*$-ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, e2
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
SYLVESTER–GALLAI TYPE THEOREMS FOR APPROXIMATE COLLINEARITY
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2014, e3
-
- Article
-
- You have access
- Open access
- Export citation
IMPROVED RANK BOUNDS FOR DESIGN MATRICES AND A NEW PROOF OF KELLY’S THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2014, e4
-
- Article
-
- You have access
- Open access
- Export citation
Computational Mathematics
Research Article
PLANE WAVE STABILITY OF THE SPLIT-STEP FOURIER METHOD FOR THE NONLINEAR SCHRÖDINGER EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2014, e5
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
DEGENERATIONS OF COMPLEX DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2014, e6
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Research Article
CONSTRUCTION OF TWO-DIMENSIONAL QUANTUM FIELD MODELS THROUGH LONGO–WITTEN ENDOMORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2014, e7
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Research Article
FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2014, e8
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
SUPERBOSONIZATION VIA RIESZ SUPERDISTRIBUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, e9
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
THE EXISTENCE THEOREM FOR THE GENERAL RELATIVISTIC CAUCHY PROBLEM ON THE LIGHT-CONE
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2014, e10
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Research Article
VORTEX LIQUIDS AND THE GINZBURG–LANDAU EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2014, e11
-
- Article
-
- You have access
- Open access
- Export citation
Computational Mathematics
Research Article
SPARSE APPROXIMATION AND RECOVERY BY GREEDY ALGORITHMS IN BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2014, e12
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
COUNTING
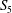 $S_5$-FIELDS WITH A POWER SAVING ERROR TERM
$S_5$-FIELDS WITH A POWER SAVING ERROR TERM
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2014, e13
-
- Article
-
- You have access
- Open access
- Export citation
SUR LES COMPOSANTES CONNEXES D’UNE FAMILLE D’ESPACES ANALYTIQUES
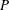 ${P}$-ADIQUES
${P}$-ADIQUES
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2014, e14
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
Multi-solitons for nonlinear Klein–Gordon equations
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2014, e15
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
Raising the level for
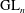 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2014, e16
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
CHOW GROUPS, CHOW COHOMOLOGY, AND LINEAR VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 24 June 2014, e17
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2014, e18
-
- Article
-
- You have access
- Open access
- Export citation
Differential Geometry and Geometric Analysis
Research Article
GEODESIC COMPLETENESS FOR SOBOLEV METRICS ON THE SPACE OF IMMERSED PLANE CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2014, e19
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
KAROUBI’S RELATIVE CHERN CHARACTER, THE RIGID SYNTOMIC REGULATOR, AND THE BLOCH–KATO EXPONENTIAL MAP
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2014, e20
-
- Article
-
- You have access
- Open access
- Export citation