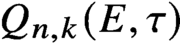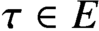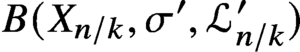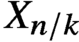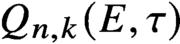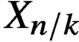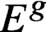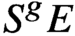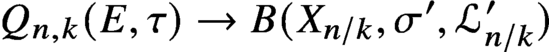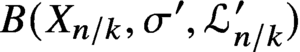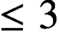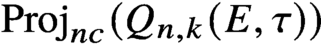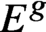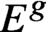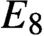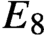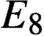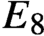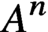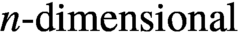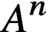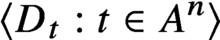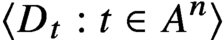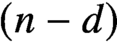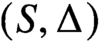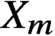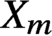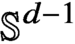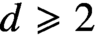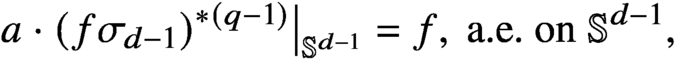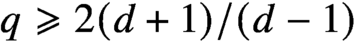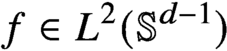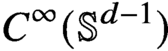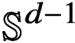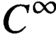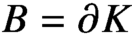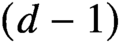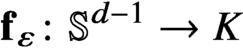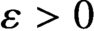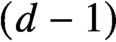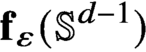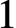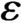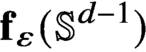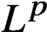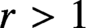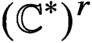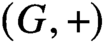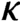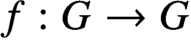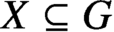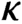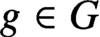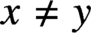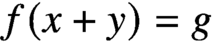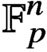Differential Equations
Strichartz estimates for orthonormal families of initial data and weighted oscillatory integral estimates
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, e1
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
On exceptional Lie geometries
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Log
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, e3
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Maps from Feigin and Odesskii's elliptic algebras to twisted homogeneous coordinate rings
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Verlinde formulae on complex surfaces: K-theoretic invariants
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, e5
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
A class of continuous non-associative algebras arising from algebraic groups including
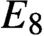 $E_8$
$E_8$
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2021, e6
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Minimal definable graphs of definable chromatic number at least three
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2021, e7
-
- Article
-
- You have access
- Open access
- Export citation
A structure theorem for stochastic processes indexed by the discrete hypercube
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2021, e8
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Curves on K3 surfaces in divisibility 2
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2021, e9
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Nonspecial varieties and generalised Lang–Vojta conjectures
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2021, e11
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Smoothness of solutions of a convolution equation of restricted type on the sphere
- Part of:
-
- Published online by Cambridge University Press:
- 07 April 2021, e12
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Continuous Maps from Spheres Converging to Boundaries of Convex Hulls
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2021, e13
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Global boundedness of a class of multilinear Fourier integral operators
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2021, e14
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Higher rank K-theoretic Donaldson-Thomas Theory of points
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2021, e15
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Transformations of the transfinite plane
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2021, e16
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Overconvergent modular forms are highest-weight vectors in the Hodge-Tate weight zero part of completed cohomology
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2021, e17
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Uniqueness of optimal symplectic connections
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2021, e18
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
High-entropy dual functions over finite fields and locally decodable codes
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2021, e19
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of:
-
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation