Article contents
Banach spaces for which the space of operators has 2𝔠 closed ideals
Published online by Cambridge University Press: 19 March 2021
Abstract
We formulate general conditions which imply that 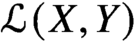 ${\mathcal L}(X,Y)$, the space of operators from a Banach space X to a Banach space Y, has
${\mathcal L}(X,Y)$, the space of operators from a Banach space X to a Banach space Y, has 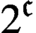 $2^{{\mathfrak {c}}}$ closed ideals, where
$2^{{\mathfrak {c}}}$ closed ideals, where 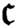 ${\mathfrak {c}}$ is the cardinality of the continuum. These results are applied to classical sequence spaces and Tsirelson-type spaces. In particular, we prove that the cardinality of the set ofclosed ideals in
${\mathfrak {c}}$ is the cardinality of the continuum. These results are applied to classical sequence spaces and Tsirelson-type spaces. In particular, we prove that the cardinality of the set ofclosed ideals in 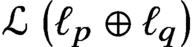 ${\mathcal L}\left (\ell _p\oplus \ell _q\right )$ is exactly
${\mathcal L}\left (\ell _p\oplus \ell _q\right )$ is exactly 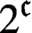 $2^{{\mathfrak {c}}}$ for all
$2^{{\mathfrak {c}}}$ for all 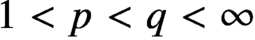 $1<p<q<\infty $.
$1<p<q<\infty $.
MSC classification
- Type
- Analysis
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
 $L\left({l}_p,{l}_q\right)$’, Studia Math. 179(3) (2007), 239–262.CrossRefGoogle Scholar
$L\left({l}_p,{l}_q\right)$’, Studia Math. 179(3) (2007), 239–262.CrossRefGoogle Scholar $L\left({\ell}_p\oplus {\ell}_q\right)$’, Oper. Matrices 6(2) (2012), 311–326.CrossRefGoogle Scholar
$L\left({\ell}_p\oplus {\ell}_q\right)$’, Oper. Matrices 6(2) (2012), 311–326.CrossRefGoogle Scholar- 2
- Cited by





