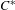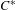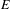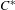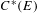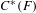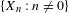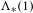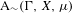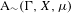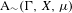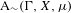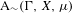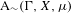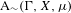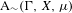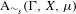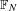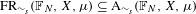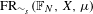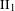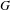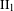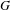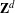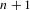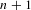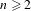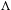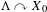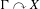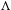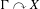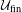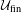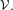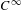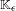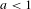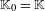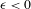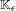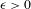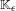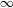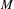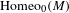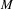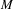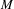We analyze the structure of the quotient 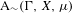 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ of the space of measure-preserving actions of a countable discrete group by the relation of weak equivalence. This space carries a natural operation of convex combination. We introduce a variant of an abstract construction of Fritz which encapsulates the convex combination operation on
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ of the space of measure-preserving actions of a countable discrete group by the relation of weak equivalence. This space carries a natural operation of convex combination. We introduce a variant of an abstract construction of Fritz which encapsulates the convex combination operation on 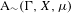 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$. This formalism allows us to define the geometric notion of an extreme point. We also discuss a topology on
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$. This formalism allows us to define the geometric notion of an extreme point. We also discuss a topology on 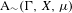 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ due to Abért and Elek in which it is Polish and compact, and show that this topology is equivalent to others defined in the literature. We show that the convex structure of
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ due to Abért and Elek in which it is Polish and compact, and show that this topology is equivalent to others defined in the literature. We show that the convex structure of 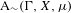 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ is compatible with the topology, and as a consequence deduce that
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ is compatible with the topology, and as a consequence deduce that 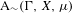 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ is path connected. Using ideas of Tucker-Drob, we are able to give a complete description of the topological and convex structure of
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ is path connected. Using ideas of Tucker-Drob, we are able to give a complete description of the topological and convex structure of 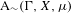 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ for amenable
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ for amenable  $\unicode[STIX]{x1D6E4}$ by identifying it with the simplex of invariant random subgroups. In particular, we conclude that
$\unicode[STIX]{x1D6E4}$ by identifying it with the simplex of invariant random subgroups. In particular, we conclude that 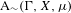 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ can be represented as a compact convex subset of a Banach space if and only if
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ can be represented as a compact convex subset of a Banach space if and only if  $\unicode[STIX]{x1D6E4}$ is amenable. In the case of general
$\unicode[STIX]{x1D6E4}$ is amenable. In the case of general  $\unicode[STIX]{x1D6E4}$ we prove a Krein–Milman-type theorem asserting that finite convex combinations of the extreme points of
$\unicode[STIX]{x1D6E4}$ we prove a Krein–Milman-type theorem asserting that finite convex combinations of the extreme points of 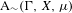 $\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ are dense in this space. We also consider the space
$\text{A}_{{\sim}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ are dense in this space. We also consider the space 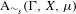 $\text{A}_{{\sim}_{s}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ of stable weak equivalence classes and show that it can always be represented as a compact convex subset of a Banach space. In the case of a free group
$\text{A}_{{\sim}_{s}}(\unicode[STIX]{x1D6E4},X,\unicode[STIX]{x1D707})$ of stable weak equivalence classes and show that it can always be represented as a compact convex subset of a Banach space. In the case of a free group 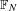 $\mathbb{F}_{N}$, we show that if one restricts to the compact convex set
$\mathbb{F}_{N}$, we show that if one restricts to the compact convex set 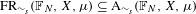 $\text{FR}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})\subseteq \text{A}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})$ consisting of the stable weak equivalence classes of free actions, then the extreme points are dense in
$\text{FR}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})\subseteq \text{A}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})$ consisting of the stable weak equivalence classes of free actions, then the extreme points are dense in 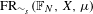 $\text{FR}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})$.
$\text{FR}_{{\sim}_{s}}(\mathbb{F}_{N},X,\unicode[STIX]{x1D707})$.
 $^{\ast }$-isomorphisms of graph
$^{\ast }$-isomorphisms of graph 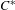 $C^{\ast }$-algebras
$C^{\ast }$-algebras
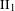 $\text{II}_{1}$ factors and stable equivalence relations
$\text{II}_{1}$ factors and stable equivalence relations